P2048 [NOI2010] Super Piano

Xiao Z is a well-known pianist. Recently, Dr. C gave Xiao Z a super piano, and Xiao Z hopes to use it to create the most beautiful music in the world. This super piano can play $n$ notes, indexed from $1$ to $n$. The beauty value of the $i$-th note is $A_i$, where $A_i$ can be positive or negative. A “super chord” consists of several consecutive notes, with the number of included notes no less than $L$ and no more than $R$. We define the beauty of a super chord as the sum of the beauty values of all notes it contains. Two super chords are considered the same if and only if the sets of notes they contain are identical. Xiao Z decides to compose a piece consisting of $k$ super chords. To make the piece more pleasing, the $k$ super chords must be different. We define the beauty of a piece as the sum of the beauties of all its super chords. Xiao Z wants to know the maximum possible beauty of such a piece. 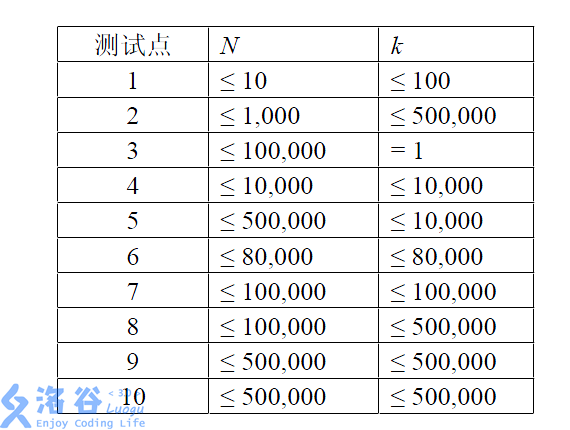All testdata satisfy: $-1000 \leq A_i \leq 1000$, $1 \leq L \leq R \leq n$, and it is guaranteed that there exists a valid piece that meets the requirements.

The first line contains four positive integers $n, k, L, R$, where $n$ is the number of notes, $k$ is the number of super chords in the piece, and $L$ and $R$ are the lower and upper bounds on the number of notes a super chord can contain, respectively. The next $n$ lines each contain an integer $A_i$, representing the beauty value of each note in increasing index order.

Output a single integer, the maximum possible beauty of the piece.

### Sample Explanation There are $5$ different super chords: 1. Notes $1 \sim 2$, beauty $3+2=5$. 2. Notes $2 \sim 3$, beauty $2+(-6)=-4$. 3. Notes $3 \sim 4$, beauty $(-6)+8=2$. 4. Notes $1 \sim 3$, beauty $3+2+(-6)=-1$. 5. Notes $2 \sim 4$, beauty $2+(-6)+8=4$. The optimal plan is: the piece consists of chords $1, 3, 5$, with total beauty $5+2+4=11$.  Translated by ChatGPT 5