P2052 [NOI2011] Road Construction

There are $n$ countries on planet W. To develop their economies, they decide to build bidirectional roads between countries so that all countries are connected. However, each king is stingy and they are only willing to build exactly $n - 1$ bidirectional roads. Building each road costs an amount equal to the road length multiplied by the absolute difference between the numbers of countries on the two sides of this road (i.e., after removing this road, in the two resulting connected components). For example, in the figure below, the dashed road has $2$ and $4$ countries on its two sides. If its length is $1$, then the cost is $1 \times |2 - 4| = 2$. The numbers inside the circles in the figure represent country indices.  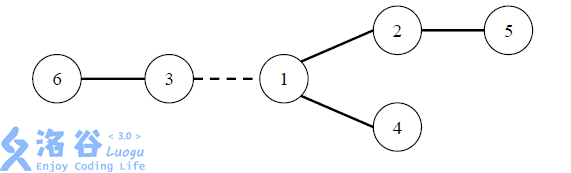Because the number of countries is very large, there are many construction schemes, and the cost of each scheme is difficult to compute by hand. The kings decide to commission software that, for a given construction scheme, computes the required total cost. Please help design such software.

The first line contains an integer $n$, the number of countries on planet W. The countries are numbered from $1$ to $n$. The next $n - 1$ lines describe the road network. The $i$-th line contains three integers $a_i$, $b_i$, and $c_i$, indicating that the $i$-th bidirectional road is built between countries $a_i$ and $b_i$, with length $c_i$.

Output a single integer, the total cost required to build all the roads.

Constraints: For $100\%$ of the testdata, $1 \leq a_i, b_i \leq n$, $0 \leq c_i \leq 10^6$, $2 \leq n \leq 10^6$. |Test point ID|$n=$| |:-:|:-:| |$1$|$2$| |$2$|$10$| |$3$|$100$| |$4$|$200$| |$5$|$500$| |$6$|$600$| |$7$|$800$| |$8$|$1000$| |$9$|$10^4$| |$10$|$2 \times 10^4$| |$11$|$5 \times 10^4$| |$12$|$6 \times 10^4$| |$13$|$8 \times 10^4$| |$14$|$10^5$| |$15$|$6 \times 10^5$| |$16$|$7 \times 10^5$| |$17$|$8 \times 10^5$| |$18$|$9 \times 10^5$| |$19,20$|$10^6$| Translated by ChatGPT 5