P2060 [HNOI2006] 马步距离
题目描述
在国际象棋和中国象棋中,马的移动规则相同,都是走“日”字,我们将这种移动方式称为马步移动。
如下图所示,从标号为 $0$ 的点出发,可以经过一步马步移动达到标号为 $1$ 的点,经过两步马步移动达到标号为 $2$ 的点。
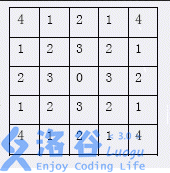
任给平面上的两点 $p$ 和 $s$,它们的坐标分别为 $(x_p,y_p)$ 和 $(x_s,y_s)$,从 $(x,y)$ 出发经过一步马步移动可以达到 $(x+1,y+2)$,$(x+2,y+1)$,$(x+1,y-2)$,$(x+2,y-1)$,$(x-1,y+2)$,$(x-2,y+1)$,$(x-1,y-2)$、$(x-2,y-1)$。
假设棋盘充分大,并且坐标可以为负数。现在请你求出从点 $p$ 到点 $s$ 至少需要经过多少次马步移动?
输入格式
输入只有一行四个用空格隔开的整数,分别代表 $x_p,y_p,x_s,y_s$。
输出格式
含一个整数,表示从点 $p$ 到点 $s$ 至少需要经过的马步移动次数。
说明/提示
#### 数据规模与约定
对于 $100\%$ 的数据,保证 $1 \leq x_p,y_p,x_s,y_s \leq 10^7$。