P2060 [HNOI2006] Knight Move Distance

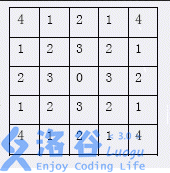
In international chess and Chinese chess (Xiangqi), the horse/knight moves in the same way, following an L shape. We call this movement a knight move. As shown in the figure below, starting from the point labeled $0$, you can reach a point labeled $1$ in one knight move, and a point labeled $2$ in two knight moves.  Given any two points $p$ and $s$ on the plane, with coordinates $(x_p,y_p)$ and $(x_s,y_s)$ respectively, from $(x,y)$ you can reach $(x+1,y+2)$, $(x+2,y+1)$, $(x+1,y-2)$, $(x+2,y-1)$, $(x-1,y+2)$, $(x-2,y+1)$, $(x-1,y-2)$, $(x-2,y-1)$ in one knight move. Assume the board is sufficiently large, and coordinates can be negative. Please compute the minimum number of knight moves needed to get from point $p$ to point $s$.

A single line containing four integers separated by spaces, representing $x_p,y_p,x_s,y_s$.

Output a single integer, the minimum number of knight moves from point $p$ to point $s$.

#### Constraints For $100\%$ of the testdata, it is guaranteed that $1 \leq x_p,y_p,x_s,y_s \leq 10^7$. Translated by ChatGPT 5