P2145 [JSOI2007] Zuma

Admin note: This problem may be flawed. 2025-01-27 update: A polynomial-time solution now exists, but it still cannot pass under the original constraints (UOJ941).

This is a game popular in JSOI, called Zuma. With its delicate visuals and mysterious Inca-style music, Zuma feels like a mystical game set in an ancient land. The protagonist is a stone frog that spits colored beads. The beads are beautifully shaped and have mysterious colors. Around the stone frog is a track carrying beads of different colors that slide forward along the track. The stone frog must stop the beads from rolling into the hole at the end of the track. How can we reduce the beads? By letting the bead shot by the frog combine with the beads on the track: if the colors match, they disappear and score points! The goal is to clear all the beads on the track. If you are not familiar with Zuma, that is fine. Here we introduce a simplified version of the rules. There is a row of glass beads in a channel, each with its own color, as shown in Figure 1. The player can choose a bead of any color (note: the color can be chosen freely; this differs from the real game) and shoot it into any position.  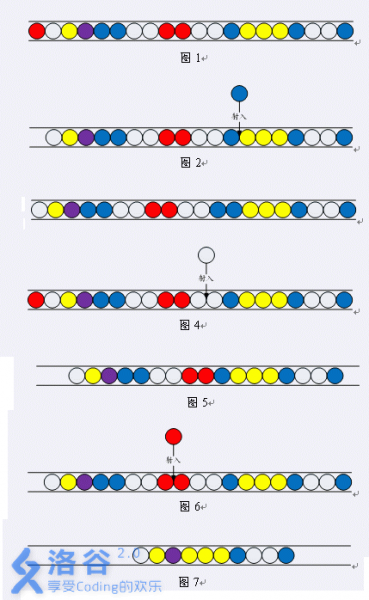In Figure 2, the player chooses a blue bead and shoots it into the indicated position, resulting in the situation in Figure 3. After a bead is shot, if the inserted bead forms a sequence of three or more consecutive beads of the same color, those beads disappear. For example, inserting a white bead at the position in Figure 4 creates three consecutive white beads. These three beads then disappear, leading to the situation in Figure 5. Note that the three consecutive yellow beads in Figure 4 do not disappear because no bead was inserted into them. Disappearance can trigger chain reactions. When a run of identical-colored beads disappears, if the beads immediately to the left and right of the vanished segment are of the same color and their combined length is greater than 2, they also disappear. For example, in Figure 6, after inserting a red bead, three consecutive red beads are formed. When the red beads disappear, both sides are white beads, four in total, so the white beads disappear as well. Afterwards, both sides are blue beads, three in total, so the blue beads also disappear. The final state is shown in Figure 7. Note that the three yellow beads in Figure 7 do not disappear because on the two sides of where the blue beads vanished there are purple beads on one side and yellow beads on the other, which are different colors. Other than the situations described above, there is no other way to eliminate beads. Now, given a row of beads, you need to clear them. On each move, you may freely choose the color of the bead and insert it at any position. Your task is to shoot the fewest number of beads to remove all beads.

The first line contains an integer $n(n \le 500)$, the number of beads. The second line contains $n$ integers (within the 32-bit integer range), separated by spaces; each integer represents the color of a bead.

Output a single integer: the minimum number of beads that must be shot.

------------ 2024/2/13: Added 2 sets of hack testdata. Translated by ChatGPT 5