P2146 [NOI2015] Software Package Manager

Linux users and OSX users are certainly familiar with package managers. With a package manager, you can install a package with a single command. The package manager will download the package from repositories and automatically resolve all dependencies (that is, download and install other packages required for this package), and finish all configurations. apt-get for Debian/Ubuntu, yum for Fedora/CentOS, and homebrew on OSX are all excellent package managers.

You decide to design your own package manager. Inevitably, you must handle dependencies between packages. If package $a$ depends on package $b$, then before installing package $a$, you must first install package $b$. Likewise, if you want to uninstall package $b$, you must uninstall package $a$. Now you have obtained all dependency relations among packages. Moreover, due to your previous design, every package in your manager except package $0$ depends on exactly one package, and package $0$ depends on none. The dependency relations contain no cycles (i.e., there do not exist $m$ packages $a_1, a_2, \dots, a_m$ such that for $i < m$, $a_i$ depends on $a_{i+1}$, and $a_m$ depends on $a_1$). You now need to write a dependency resolver for your package manager. According to user feedback, when installing or uninstalling a package, users want to quickly know how many packages will actually change their installation state as a result of the operation (that is, how many currently uninstalled packages will be installed by an install operation, or how many currently installed packages will be uninstalled by an uninstall operation). Your task is to implement this part. Note that installing an already installed package, or uninstalling a package that is not installed, will not change any installation state. In this case, the number of packages whose installation state changes is $0$.

The first line contains a positive integer $n$, the number of packages, numbered starting from $0$. The second line contains $n - 1$ integers; the $i$-th integer denotes the package ID that package $i$ depends on. Then a line with a positive integer $q$ follows, denoting the number of operations, in the following format: - `install x` means install package $x$. - `uninstall x` means uninstall package $x$. Initially, all packages are not installed. For each operation, you need to output how many packages will change their installation state because of this step, and then apply the operation (i.e., update the installation states you maintain).

Output $q$ lines, each containing an integer, which is the answer for each query.

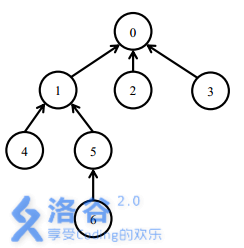
 Initially, all packages are not installed. To install package $5$, you need to install packages $0, 1, 5$. After that, installing package $6$ only requires installing package $6$. At this point, packages $0, 1, 5, 6$ are installed. Uninstalling package $1$ requires uninstalling packages $1, 5, 6$. Now only package $0$ remains installed. Next, installing package $4$ requires installing packages $1, 4$. Now packages $0, 1, 4$ are installed. Finally, uninstalling package $0$ will uninstall all packages. **Constraints** ::cute-table{tuack} | Test point ID | $$n$$ size | $$q$$ size | Notes | |:-------------:|:-------------------:|:-------------------:|:-----:| | $1$ | ${n = 5{,}000}$ | ${q = 5{,}000}$ | | | $2$ | ^ | ^ | ^ | | $3$ | ${n = 100{,}000}$ | ${q = 100{,}000}$ | testdata does not include uninstall operations | | $4$ | ^ | ^ | ^ | | $5$ | ${n = 100{,}000}$ | ${q = 100{,}000}$ | For package $i$, the ID of the package it depends on is uniformly random in $[0, i - 1]$, and the package ID in each operation is uniformly random in $[0, n - 1]$. | | $6$ | ^ | ^ | ^ | | $7$ | ^ | ^ | ^ | | $8$ | ^ | ^ | ^ | | $9$ | ${n = 100{,}000}$ | ${q = 100{,}000}$ | | | $10$ | ^ | ^ | ^ | | $11$ | ^ | ^ | ^ | | $12$ | ^ | ^ | ^ | | $13$ | ^ | ^ | ^ | | $14$ | ^ | ^ | ^ | | $15$ | ^ | ^ | ^ | | $16$ | ^ | ^ | ^ | | $17$ | ^ | ^ | ^ | | $18$ | ^ | ^ | ^ | | $19$ | ^ | ^ | ^ | | $20$ | ^ | ^ | ^ | Translated by ChatGPT 5