P2154 [SDOI2009] The Devout Grave Keeper

Xiao W is the manager of a newly built cemetery. The cemetery can be regarded as an $N×M$ rectangle. Each lattice point is either planted with an evergreen tree, or is a grave plot that has not yet been assigned. The local residents are very devout Christians, and they are willing to choose a suitable grave plot for themselves in advance. To show their sincerity to the Lord, they hope their grave plot has a high level of piety. The piety of a grave plot is defined as the number of crosses centered at this plot. A cross consists of a center grave plot, and exactly $k$ evergreen trees immediately above, below, left, and right of it. Formally, for a grave plot at coordinates $(x, y)$, the number of crosses centered at it is the number of sequences of length $4k$ of ordered pairs $[(x_{1,1},y_{1,1}),\allowbreak(x_{1,2},y_{1,2}),\allowbreak\cdots,(x_{1,k},y_{1,k}),\allowbreak(x_{2,1},y_{2,1}),\allowbreak(x_{2,2},y_{2,2}),\allowbreak\cdots,(x_{2,k},y_{2,k}),\allowbreak(x_{3,1},y_{3,1}),\allowbreak(x_{3,2},y_{3,2}),\allowbreak\cdots,(x_{3,k},y_{3,k}),\allowbreak(x_{4,1},y_{4,1}),\allowbreak(x_{4,2},y_{4,2}),\allowbreak\cdots,(x_{4,k},y_{4,k})]$ that satisfy: - Each ordered pair corresponds to the coordinates of an evergreen tree. - $x_{1,1}

The first line contains two positive integers $N$ and $M$, representing the width and length of the cemetery. Therefore, this rectangular cemetery has $(N+1) ×(M+1)$ lattice points, with the lower-left corner at $(0, 0)$ and the upper-right corner at $(N, M)$. The second line contains a positive integer $W$, representing the number of evergreen trees in the cemetery. From the third line, there are $W$ lines. Each line contains two non-negative integers $x_i$ and $y_i$, representing the coordinates of an evergreen tree. The input guarantees that no two evergreen trees have the same coordinates. The last line contains a positive integer $k$, as defined in the statement.

Output a single non-negative integer, which is the sum of the piety levels over all grave plots in this cemetery. For convenience, output the answer modulo $2{,}147{,}483{,}648$.

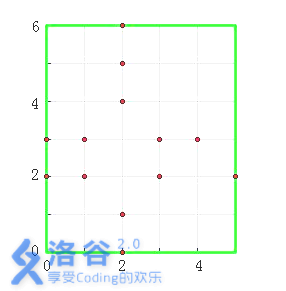
In the figure, the number of crosses centered at grave plots $(2, 2)$ and $(2, 3)$ is $3$, so their piety levels are both $3$. The piety level of every other grave plot is $0$.  For $30\%$ of the testdata, $1 ≤ N, M ≤ 10^3$. For $60\%$ of the testdata, $1 ≤ N, M ≤ 10^6$. For $100\%$ of the testdata, $1 ≤ N, M ≤ 10^9$，$0 ≤ x_i ≤ N$，$0 ≤ y_i ≤ M$，$1 ≤ W ≤ 10^5$，$1 ≤ k ≤ 10$。 There exists $50\%$ of the testdata such that $1 ≤ k ≤ 2$. There exists $25\%$ of the testdata such that $1 ≤ W ≤ 10^4$. Translated by ChatGPT 5