P2162 [SHOI2007] 宝石纪念币
题目描述
Constantine 刚结束在 MySky Island 的度假,正准备离开的时候,他想送给她的好朋友 YY 一份特别的礼物——MySky Island 上特别的手工艺品宝石纪念币。
宝石纪念币的一面上刻着小岛的名字 `MySky`,或者收礼物的人,比如 `to YY`。不过特别的是,每枚纪念币的反面,依次均匀的镶着一圈共 $n$ 颗彩色的宝石。
例如,下面是一个 $n=7$ 时的简单例子:
因为纪念币是圆的,所以如果两种“宝石颜色的排布”经过旋转后对应位置的颜色相重合,就认为它们是相同的排布方式。
(请注意:纪念币只有一面镶宝石,所以两种排布若经过翻转以后是可以重合的,但只经过旋转无法使两者重合,则认为他们是不同的排布。)
例如下面的两种排布方式就是相同的:
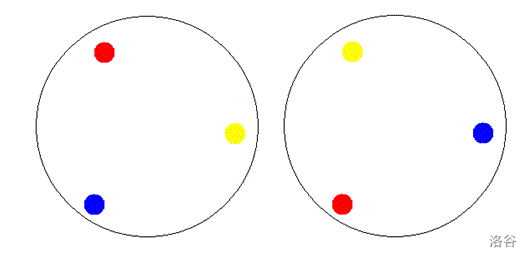
另外,由于 MySky Island 当地的习俗,每枚钱币上都只能嵌奇数颗宝石,不然就认为是不吉利的。
宝石纪念币是现场制作的,游客可以选择自己喜欢的颜色的宝石。所以 Constantine 选出了他最喜欢的 $17$ 种颜色(你如果要问为什么选这么多的话,只能告诉你因为 $17$ 是他的幸运数字)。他想知道,如果按他要求把这 ${17}$ 种颜色的宝石都用上的话,可以制作出多少枚不同的纪念币。
由于答案可能很大,你只需要计算答案的最后 $120$ 位(十进制)就可以了。
输入格式
一行一个正奇数 $n\ (1 \le n \le 10^9-1)$。
输出格式
一行 $120$ 个数字字符,表示不同纪念币的枚数的最后 $120$ 位。这 $120$ 位从高位到低位依次输出,位数不足的用 $0$ 在高位补足。