P2162 [SHOI2007] Gem Commemorative Coin

Constantine has just finished his vacation on MySky Island. As he is about to leave, he wants to give his good friend YY a special gift—a handcrafted gem commemorative coin from MySky Island. One side of the coin is engraved with the island’s name “MySky,” or the recipient’s name, for example, “to YY.” What is special is that on the reverse side, there are $n$ colored gems evenly embedded in a circle. 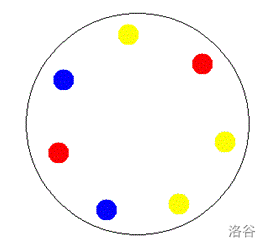For example, here is a simple example for $n=7$:  Since the coin is circular, two “color arrangements of the gems” are considered the same if they can be made to match by a rotation. 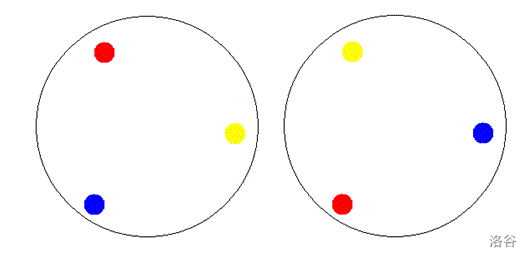(Please note: the gems are embedded on only one side of the coin. Therefore, two arrangements that can be made to match by a reflection but not by any rotation are considered different.) For example, the following two arrangements are the same:  Additionally, due to local custom on MySky Island, only coins with an odd number of gems are considered auspicious. The gem coins are made on site, and tourists can choose the colors they like. Constantine picked his 17 favorite colors (if you ask why so many, it’s because 17 is his lucky number). He wants to know, if all these 17 colors must be used, how many different coins can be made. Since the answer can be very large, you only need to compute the last 120 digits (in decimal).

One line with an odd positive integer $n$ ($1 \le n \le 10^9 - 1$).

One line with 120 digit characters, representing the last 120 digits of the number of distinct coins. Output the digits from most significant to least significant; if the number has fewer than 120 digits, pad with leading zeros on the left.

Translated by ChatGPT 5