P2173 [ZJOI2012] Network

There is an undirected graph $G$. Each node has a weight, and each edge has a color. This undirected graph satisfies the following two conditions: 1. For any node, among all edges incident to it, there are at most two edges of the same color. 2. There is no monochromatic cycle in the graph, i.e., no cycle formed by edges of the same color. On this graph, you need to support the following three operations: - `0 x y` means set the weight of node $x$ to $y$. - `1 u v w` means change the color of edge $(u, v)$ to $w$. - `2 c u v` means query, in the subgraph formed by edges of color $c$, the maximum weight among all nodes that lie on any simple path from $u$ to $v$.

The first line contains four positive integers $n, m, C, k$, denoting the number of nodes, the number of edges, the number of colors, and the number of operations, respectively. The next $n$ lines each contain one positive integer $v_i$, the weight of node $i$. The next $m$ lines each contain three positive integers $u, v, w$, denoting an edge connecting nodes $u$ and $v$ with color $w$. The last $k$ lines each contain several positive integers, representing one operation.

Output several lines, each containing the corresponding message. 1. For node weight modification operations, no output is required. 2. For edge color modification operations, print one of the following: - If there is no edge connecting node $u$ and node $v$, print `No such edge.`. - If the modification would violate condition 1, do not modify the edge color and print `Error 1.`. - If the modification would violate condition 2, do not modify the edge color and print `Error 2.`. - Otherwise, modify the edge color successfully and print `Success.`. Only print the first applicable message. That is, if both conditions 1 and 2 would be violated, print only `Error 1.`. 3. For query operations, print one integer as the answer. If there is no path of color $c$ between $u$ and $v$, print $-1$.

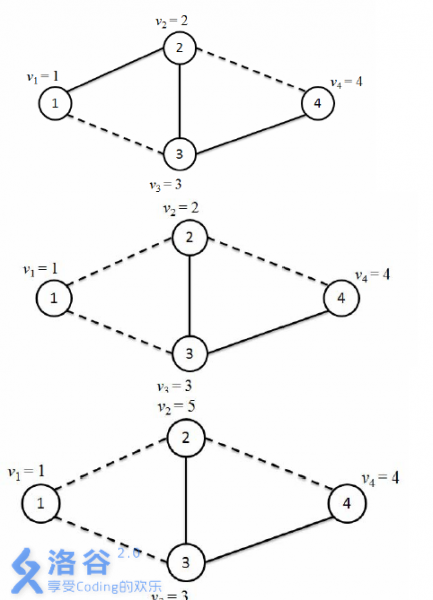
 Edges of color $0$ are solid; edges of color $1$ are dashed. In the subgraph formed by edges of color $0$, there is a path from node $1$ to node $4$: $1 \to 2 \to 4$. Thus $\max\{ v_1, v_2, v_4 \} = \max\{ 1, 2, 4 \} = 4$. Changing the edge between nodes $1$ and $2$ to color $1$ succeeds, so print `Success.`. Changing the edge between nodes $4$ and $3$ to color $1$ would create a monochromatic cycle of color $1$ ($1 – 2 – 4 – 3 – 1$), violating condition 2, so do not modify it and print `Error 2.`. There is no path of color $0$ from node $1$ to node $4$, so print $-1$. Changing the edge between nodes $2$ and $3$ to color $1$ would make node $2$ incident to three edges of color $1$, violating condition 1, so do not modify it and print `Error 1.`. Change the weight of node $2$ to $5$. In the subgraph formed by edges of color $1$, there is a path from node $1$ to node $4$: $1 \to 2 \to 4$. Thus $\max\{ v_1, v_2, v_4 \} = \max\{ 1, 5, 4 \} = 5$. Constraints - For $30\%$ of the testdata: $n \le 1000$, $m \le 10^4$, $k \le 1000$. - Additionally, for $20\%$ of the testdata: $n \le 10^4$, $m \le 10^5$, $C = 1$, $k \le 10^5$. - For $100\%$ of the testdata: $n \le 10^4$, $m \le 10^5$, $C \le 10$, $k \le 10^5$. $1 \le u, v, x \le n$, $0 \le c < C$. There are no multiple edges or self-loops in the graph. Translated by ChatGPT 5