P2178 [NOI2015] Wine Tasting Convention

The annual "Phantom Pavilion Summer Wine Tasting Convention" has grandly opened. The convention consists of two parts: tasting and a fun challenge. They award two titles, "Chief Taster" and "Chief Hunter", attracting many sommeliers to participate. At the dinner, the bartender Rainbow mixed $n$ cocktails. These $n$ cocktails are arranged in a line. The $i$-th glass ($1 \le i \le n$) is labeled $s_i$, where each label is one of the $26$ lowercase English letters. Let $str(l, r)$ denote the string formed by concatenating the $r - l + 1$ labels from the $l$-th glass to the $r$-th glass in order. If $str(p, p_0) = str(q, q_0)$, where $1 \le p \le p_0 \le n$, $1 \le q \le q_0 \le n$, $p \ne q$, and $p_0 - p + 1 = q_0 - q + 1 = r$, then we say the $p$-th glass and the $q$-th glass are r-similar. Of course, if two glasses are r-similar (with $r > 1$), then they are also 1-similar, 2-similar, …, and $(r - 1)$-similar. In particular, for any $1 \le p, q \le n$, $p \ne q$, the $p$-th and the $q$-th glasses are 0-similar. In the tasting part, the sommelier Freda easily evaluated the deliciousness of each glass and won the title of "Chief Taster" with her professional skill and experience. The deliciousness of the $i$-th glass ($1 \le i \le n$) is $a_i$. Now Rainbow announces the challenge: the cocktails in this convention have a special property—if you mix the $p$-th glass with the $q$-th glass, you obtain a glass with deliciousness $a_p \times a_q$. For each $r = 0, 1, 2, \dots, n - 1$, please count how many ways there are to choose two r-similar glasses, and report the maximum deliciousness obtainable by mixing two r-similar glasses.

The first line contains a positive integer $n$, the number of glasses. The second line contains a string $S$ of length $n$, where the $i$-th character is the label of the $i$-th glass. The third line contains $n$ integers separated by single spaces, where the $i$-th integer is the deliciousness $a_i$ of the $i$-th glass.

Output $n$ lines. On the $i$-th line, output two integers separated by a single space. The first integer is the number of ways to choose two $(i - 1)$-similar glasses, and the second integer is the maximum deliciousness obtainable by mixing two $(i - 1)$-similar glasses. If there are no two $(i - 1)$-similar glasses, output $0 0$.

[Sample explanation 1] Use an ordered pair $(p, q)$ to denote the $p$-th glass and the $q$-th glass. 0-similar: all $45$ ordered pairs are 0-similar, and the maximum deliciousness is $8 \times 7 = 56$. 1-similar: $(1, 8) (2, 4) (2, 9) (4, 9) (5, 6) (5, 7) (5, 10) (6, 7) (6, 10) (7, 10)$, with maximum $8 \times 7 = 56$. 2-similar: $(1, 8) (4, 9) (5, 6)$, with maximum $4 \times 8 = 32$. There are no 3-, 4-, 5-, …, 9-similar pairs of glasses, so output $0$.  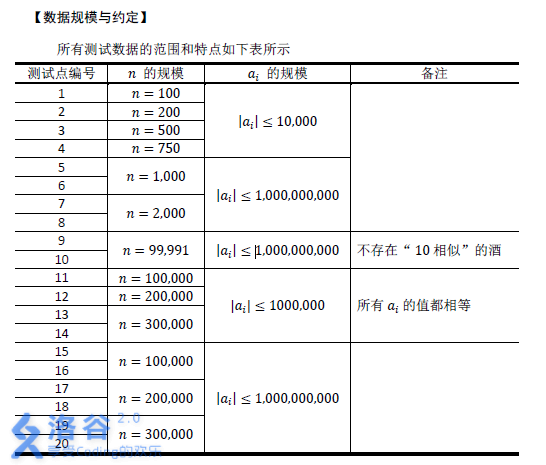[Time limit 1 s, Memory limit 500 MB] Translated by ChatGPT 5