P2225 [HNOI2001] Board Transformation

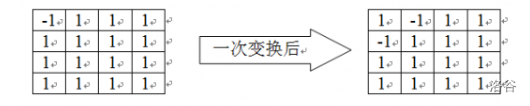
On an $n \times n$ board, fill each cell with $1$ or $-1$. After one transformation, every number in the grid becomes the product of the four numbers that are adjacent to it (up, down, left, and right) before the transformation. For example:  However, some states remain the same before and after the transformation, such as the state where all entries are $1$. Such a state is called an invariant state. Your task is to find all essentially different invariant states (states that become identical after rotations or reflections are considered essentially the same).

One line containing a single positive integer $n$.

One line containing a single positive integer, the number of essentially different invariant states.

$1 \le n \le 30$. Within the given range, the total number of invariant states is $< 9 \times 10^3$. Translated by ChatGPT 5