P2226 [HNOI2001] Remote-Controlled Car Race

The National Remote-Controlled Car Championship was recently held in Xingsha. The competition uses a field of size $N \times M$ as the course, and the requirement is for the car to move from the start to the finish in the shortest time. Although the terrain has slight undulations, there are no inherently unreachable locations. However, many impassable obstacles have been added to the course. If the car hits an obstacle before reaching the finish, the attempt is considered a failure. When the cars’ horsepower and agility are similar, the key to guiding a high-speed car around obstacles to the finish is improving the driver’s reaction sensitivity, namely the minimum time interval between two direction changes, also called the driver’s reaction time. This determines how quickly the driver can control the car to change its direction of motion. 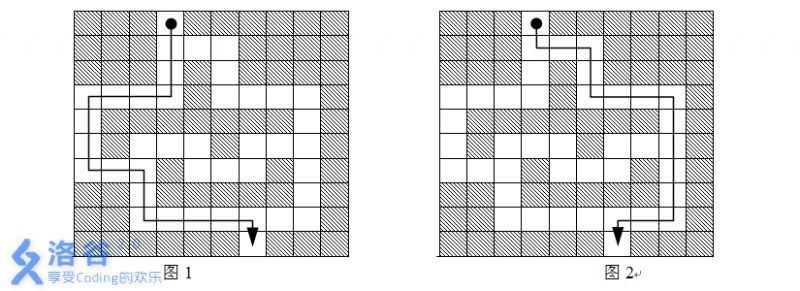Naturally, due to different reaction sensitivities, the set of feasible paths varies. As shown in Figures $1$ and $2$, for the same course, two drivers with reaction times of $2$ seconds and $1$ second, respectively, need $18$ seconds and $16$ seconds to reach the finish (the car moves one cell per second along its current direction, and the departure from the start counts as one direction change). From Figures $1$ and $2$, we see that the shortest route length depends on the driver’s reaction sensitivity. When the reaction is slow, a feasible path may not exist. Your task is: under the condition that the course can be completed (i.e., a path from the start to the finish exists), compute the shortest route length corresponding to each possible reaction time. 

The first line contains two integers $N$ and $M$, the numbers of rows and columns of the course, with $1 \le N, M \le 100$. The second line contains four integers $x1$, $y1$, $x2$, $y2$, indicating that the start and finish are located at $(x1, y1)$ and $(x2, y2)$, respectively. The next $N$ lines give a $N \times M$ 0-1 matrix. In this matrix, the element in row $i$, column $j$ is $A_{i,j} = 1$ if position $(i, j)$ is track (traversable), and $A_{i,j} = 0$ if position $(i, j)$ has an obstacle.

The output may contain multiple lines. Each line should output one possible reaction time and the corresponding shortest route length. The output must include all reaction times that meet the problem’s requirement. Note: because excessively slow reactions are not considered, you do not need to handle reaction times greater than $10$ seconds; only output solutions for reaction times up to and including $10$.

Translated by ChatGPT 5