P2233 [HNOI2002] Bus Routes

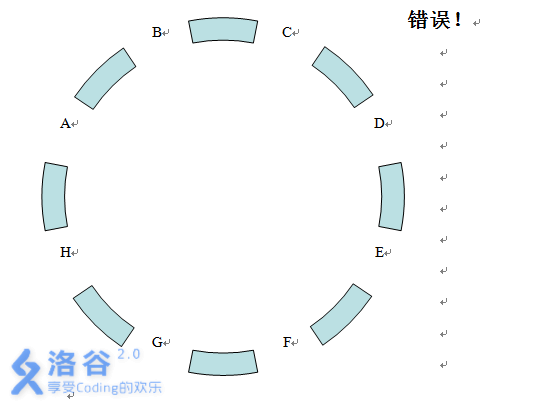
On the newly built ring road in Changsha, there are $8$ bus stops: A, B, C, D, E, F, G, H. Buses can only run between two adjacent stops. Therefore, to go from one stop to another, you often have to change buses several times. For example, to get from stop A to stop D, you need to change buses at least $3$ times.  Tiger has a very poor sense of direction. We know that to get from bus stop A to bus stop E, it takes only $4$ changes to arrive, but Tiger changed buses a total of $n$ times. Note that once Tiger reaches bus stop E, he will not be foolish enough to transfer again. Now, please compute how many possible riding plans Tiger may have.

A single positive integer $n$, indicating that Tiger changed buses a total of $n$ times from bus stop A to bus stop E.

Output a single integer representing the number of plans. Since the number may be large, output the remainder after dividing by $1000$.

The $8$ routes are: (A→B→C→D→C→D→E), (A→B→C→B→C→D→E), (A→B→A→B→C→D→E), (A→H→A→B→C→D→E), (A→H→G→F→G→F→E), (A→H→G→H→G→F→E), (A→H→A→H→G→F→E), (A→B→A→H→G→F→E). Constraints: $4\le n\le10^7$. Translated by ChatGPT 5