P2254 [NOI2005] Gorgeous Waltz

Do you dance the waltz? When the music starts and you glide with the melody, do you feel the ease of strolling in a fairyland? As everyone knows, for a waltz, the most important thing is good music. But few people know that the greatest pianist in the world drifted on the sea all his life. His name was Danny Boodman T.D. Lemon 1900, and his friends called him 1900. 1900 was born in the first year of the 20th century on the transatlantic liner Virginia. Unfortunately, he was abandoned at birth and became an orphan. He grew up alone on the Virginia and never left this swaying world. Perhaps as compensation for his fate, God sent a lovely little angel, Emily, to watch over him. Maybe it was the angel’s enlightenment that gave 1900 an incredible gift for the piano: no one taught him, and he had never seen sheet music, yet he could play the most touching melodies purely by feeling. When the music of 1900 won the hearts of everyone on the ship, he was only 8 years old, and by then he had already crossed the Atlantic more than 50 times. Although a piano prodigy, 1900 was still a child, with the same curiosity and playfulness as any boy, but with an extra touch of romance: it was a stormy night, the sea wind whipped up waves that pounded the Virginia, and the liner swayed violently with the swell. The new saxophonist on board, Max Tooney, was seasick. 1900 invited Tooney to sit with him on the piano in the ballroom, then released the brake that fixed the piano. The piano began to slide with the ship’s tilt. To be precise, our protagonist 1900…

Assume the ballroom is an $N$-by-$M$ grid. Some cells have furniture piled on them, and the rest are empty. The piano can slide on empty cells, but it cannot hit furniture or slide out of the ballroom; otherwise, both the piano and the furniture would be damaged, and the captain would be upset. At each moment, the piano slides one cell to an adjacent cell in the direction of the ship’s tilt. The adjacent cell can be east, west, south, or north. Emily can choose to cast magic or not: if she does not cast magic, the piano slides; if she does, the piano stays where it is. Emily is an angel, and she knows the ship’s tilt over each time interval. She wants to make the piano travel as long a distance as possible in the ballroom, which will make 1900 very happy and also help Tooney’s seasickness. But Emily is still too young to calculate it, so she hopes you can help her.

The first line contains 5 numbers $N$, $M$, $x$, $y$ and $K$. $N$ and $M$ describe the size of the ballroom, and $x$ and $y$ are the initial position of the piano. We describe the ship’s tilt by time intervals, and time starts from $1$. For example: “tilting east during $[1, 3]$, and tilting north during $[4, 5]$”. Therefore, $K$ is the number of intervals. The next $N$ lines, each with $M$ characters, describe the furniture in the ballroom. In row $i$, column $j$, if the character is `.` then that cell is empty; if it is `x` then there is furniture. The next $K$ lines describe the $K$ time intervals in order, in the format: $s_i\ t_i\ d_i$ ($1 \leq i \leq K$). It means that during the time interval $[s_i, t_i]$, the ship tilts toward direction $d_i$. $d_i$ is one of $1$, $2$, $3$, $4$, which denote north, south, west, and east respectively (corresponding to up, down, left, and right in the grid). The input guarantees that the intervals are continuous, that is, $s_1 = 1$, $s_i = t_{i-1} + 1$ ($1 < i \leq K$), $t_K = T$.

Output a single line containing one integer, the maximum sliding distance of the piano (i.e., the number of cells).

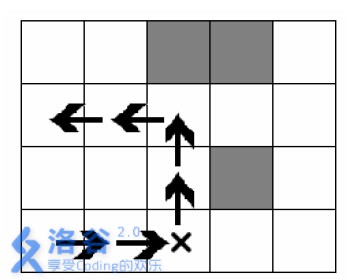
The piano’s sliding path:  When the piano is at the "×" position, the angel uses magic once, so the total sliding length is $6$. Constraints: - For $50\%$ of the testdata, $1 \leq N, M \leq 200$, $T \leq 200$. - For $100\%$ of the testdata, $1 \leq N, M \leq 200$, $K \leq 200$, $T \leq 40000$. Translated by ChatGPT 5