P2296 [NOIP 2014 Senior] Finding the Road

NOIP 2014 Senior D2T2.

In a directed graph $G$ where every edge has length $1$, you are given a start and a terminal. Please find a path from the start to the terminal that satisfies the following conditions: 1. For every vertex on the path, all endpoints of its outgoing edges are directly or indirectly able to reach the terminal. 2. Among all paths satisfying condition 1, the path should be the shortest. Note: Graph $G$ may contain multiple edges and self-loops. It is guaranteed that the terminal has no outgoing edges. Please output the length of a path that satisfies the conditions.

The first line contains two integers $n$ and $m$ separated by a space, denoting that the graph has $n$ vertices and $m$ edges. Each of the next $m$ lines contains two integers $x, y$ separated by a space, indicating there is a directed edge from vertex $x$ to vertex $y$. The last line contains two integers $s, t$ separated by a space, indicating that the start is $s$ and the terminal is $t$.

Output a single line containing an integer, the length of the shortest path that satisfies the problem statement. If such a path does not exist, output $-1$.

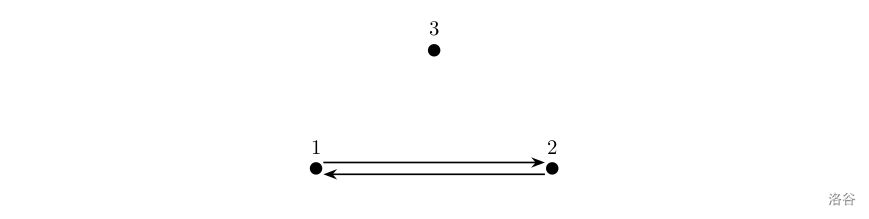
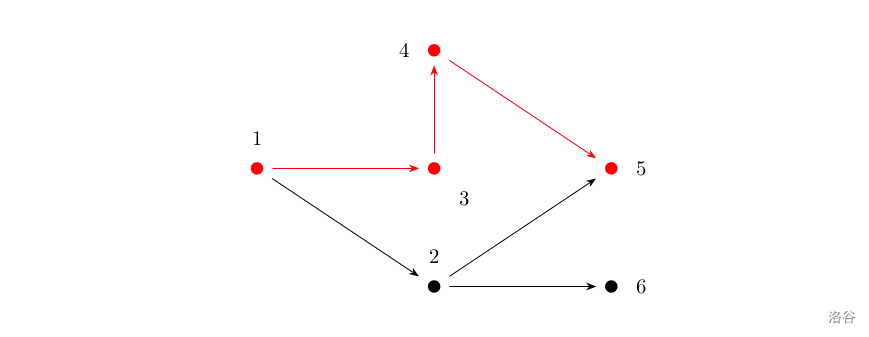
Sample 1 Explanation.  As shown in the figure above, arrows represent directed roads and dots represent cities. The start $1$ is not connected to the terminal $3$, so a path satisfying the problem statement does not exist, hence the output is $-1$. Sample 2 Explanation.  As shown in the figure above, a path that satisfies the conditions is $1 \to 3 \to 4 \to 5$. Note that vertex $2$ cannot appear in the answer path because vertex $2$ has an edge to vertex $6$, and vertex $6$ cannot reach the terminal $5$. Constraints. - For 30% of the testdata, $0 < n \le 10$, $0 < m \le 20$. - For 60% of the testdata, $0 < n \le 100$, $0 < m \le 2000$. - For 100% of the testdata, $0 < n \le 10^4$, $0 < m \le 2 \times 10^5$, $0 < x, y, s, t \le n$, $x, s \ne t$. Translated by ChatGPT 5