P2304 [NOI2015] The Little Gardener and the Veteran Driver
Description
The little gardener Mr. S is in charge of a field, which can be regarded as a 2D plane. There are $n$ wishing trees in the field, numbered $1, 2, 3, \dots, n$. Each tree is considered a point on the plane, where the $i$-th tree $(1 \leq i \leq n)$ is located at coordinates $(x_i, y_i)$. No two trees share the same coordinates.
The veteran driver Mr. P starts driving from the origin $(0,0)$ and takes several rounds of actions. In each round, Mr. P first chooses any direction that satisfies the following conditions:
1. It is one of the five directions: left, right, up, up-left $45\degree$, or up-right $45\degree$.
2. Moving along this direction can reach a tree at which he has not yet made a wish.
After making the choice, Mr. P moves straight along that direction and must reach the nearest unvisited tree in that direction, make a wish under the tree, and then proceed to the next round. If there is no direction that satisfies the conditions, he stops. He will adopt an optimal strategy to make wishes under as many trees as possible. If the optimal strategy is not unique, he may choose any one.
Unfortunately, the little gardener Mr. S finds that due to the soft soil of the field, Mr. P’s car leaves a rut during each move. A rut can be regarded as a line segment with endpoints at two trees (or the origin and a tree).
After Mr. P, many other wishers plan to drive to the field to make wishes, and they will act using some optimal strategy just like Mr. P. Mr. S believes that ruts in non-left/right directions (that is, up, up-left $45\degree$, and up-right $45\degree$) are unsightly. To maintain the appearance of the field, he plans to rent some road rollers to compact all ground that “could possibly have non-left/right-direction ruts” before these wishers arrive. The ground that “could possibly have non-left/right-direction ruts” should be a set of line segments, each contained in the route of some optimal strategy. Each road roller operates under the following three conditions:
1. It starts from the origin or any tree.
2. It can only move in one of the three directions: up, up-left $45\degree$, or up-right $45\degree$, and it may only change direction or stop at trees.
3. It can only pass through ground that “could possibly have non-left/right-direction ruts”; however, the same ground may be traversed by multiple road rollers.
Now Mr. P and Mr. S each pose a question to you:
1. Please provide Mr. P with any one optimal route.
2. Please tell Mr. S the minimum number of road rollers needed.
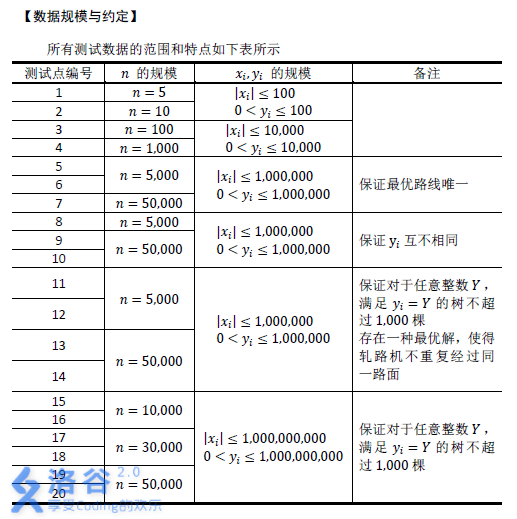
Input Format
The first line contains one positive integer $n$, the number of wishing trees.
The next $n$ lines, the $(i+1)$-th line contains $2$ integers $x_i, y_i$ separated by a single space, representing the coordinates of the $i$-th wishing tree.
Output Format
Output $3$ lines.
The first line outputs one integer $m$, the maximum number of trees under which Mr. P can make wishes.
The second line outputs $m$ integers separated by single spaces, indicating the indices of the trees where Mr. P should make wishes in order.
The third line outputs one integer, the minimum number of road rollers that Mr. S needs to rent.
Explanation/Hint
#### Explanation for Sample 1
There are $2$ optimal routes, allowing $3$ wishes: $(0,0) \rightarrow (1,1) \rightarrow (-1,1) \rightarrow (-2,2)$ or $(0,0) \rightarrow (0,8) \rightarrow (0,9) \rightarrow (0,10)$.
At least $3$ road rollers are needed, with routes $(0,0) \rightarrow (1,1)$, $(-1,1) \rightarrow (-2,2)$, and $(0,0) \rightarrow (0,8) \rightarrow (0,9) \rightarrow (0,10)$.
#### Explanation for Sample 2
The optimal route is unique: $(0,0) \rightarrow (0,1) \rightarrow (-2,1) \rightarrow (2,1) \rightarrow (3,2)$, allowing $4$ wishes. After making a wish at $(0,1)$, starting from $(-2,1)$ and heading right, the nearest unvisited tree reachable is $(2,1)$, so one can reach $(2,1)$.
If instead one proceeds as $(0,0) \rightarrow (0,1) \rightarrow (2,1) \rightarrow (-2,1)$, then at this point all trees to the right of $(-2,1)$ have already been visited. According to the rules, one must stop. Hence the optimal solution cannot be achieved.
$(0,0) \rightarrow (0,1)$ and $(2,1) \rightarrow (3,2)$ would leave non-left/right-direction ruts, so $2$ road rollers are needed.
Translated by ChatGPT 5