P2305 [NOI2014] Buying Tickets

This summer, NOI celebrated its 30th anniversary in SZ City. OIers from $n$ cities across the country will depart from their homes to attend the event in SZ City. All cities form a rooted tree with SZ City as the root, and each city is connected to its parent by a road. For convenience, we number the $n$ cities with integers from $1$ to $n$, where the number of SZ City is $1$. For any city $v$ other than SZ City, we are given its parent city $f_v$ in this tree and the length $s_v$ of the road to its parent. To travel from city $v$ to SZ City, the method is as follows: choose an ancestor $a$ of city $v$, pay for a ticket, and take a vehicle to $a$. Then choose an ancestor $b$ of city $a$, pay, and reach $b$. Repeat this process until you arrive at SZ City. For any city $v$, we are given a distance limit $l_v$ for its transportation. For an ancestor $A$ of city $v$, city $v$ can reach $A$ with a single ticket if and only if the total length of all roads along the path between them does not exceed $l_v$; otherwise, it cannot reach $A$ with a single ticket. For each city $v$, we are also given two non-negative integers $p_v, q_v$ as fare parameters. If the total length of all roads from city $v$ to city $A$ is $d$, then the price of the ticket from city $v$ to city $A$ is $d p_v + q_v$. OIers in each city want to minimize the total amount of money spent on tickets when traveling to SZ City. Your task is to tell the OIers in each city their minimum total cost.

The first line contains two non-negative integers $n, t$, denoting the number of cities and the testdata type (its meaning is mentioned in “Hint”). The next lines $2 \sim n$ each describe a city other than SZ City. Specifically, line $v$ contains five non-negative integers $f_v, s_v, p_v, q_v, l_v$, denoting the parent city of city $v$, the length of the road to its parent, the two fare parameters, and the distance limit, respectively. Note: The input does not include SZ City with number $1$. Lines $2 \sim n$ describe cities $2$ to $n$.

The output contains $n - 1$ lines, each with an integer. The $v$-th line gives the minimum total ticket cost to reach SZ City starting from city $v + 1$. Likewise, note that SZ City with number $1$ is not included in the output.

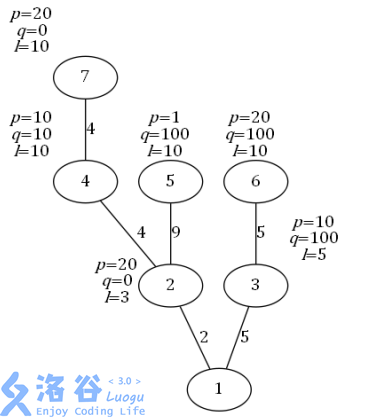
The routes from each city to SZ City are as follows (an arrow denotes a single direct trip): City $2$: Can only choose $2 \rightarrow 1$, with cost $2 \times 20 + 0 = 40$. City $3$: Can only choose $3 \rightarrow 1$, with cost $5 \times 10 + 100 = 150$. City $4$: Since $4 + 2 = 6 \leq l_4 = 10$, it can choose $4 \rightarrow 1$. If choosing $4 \rightarrow 1$, the cost is $(4 + 2) \times 10 + 10 = 70$; if choosing $4 \rightarrow 2 \rightarrow 1$, the cost is $(4 \times 10 + 10) + (2 \times 20 + 0) = 90$. Therefore, choose $4 \rightarrow 1$. City $5$: Can only choose $5 \rightarrow 2 \rightarrow 1$, with cost $(9 \times 1 + 100) + (2 \times 20 + 0) = 149$. It cannot choose $5 \rightarrow 1$ because $l_5 = 10$, while the total distance from city $5$ to city $1$ is $9 + 2 = 11 \gt 10$, so city $5$ cannot reach city $1$ directly. City $6$: If choosing $6 \rightarrow 1$, the cost is $(5 + 5) \times 20 + 100 = 300$; if choosing $6 \rightarrow 3 \rightarrow 1$, the cost is $(5 \times 20 + 100) + (5 \times 10 + 100) = 350$. Therefore, choose $6 \rightarrow 1$. City $7$: Choose $7 \rightarrow 4 \rightarrow 1$, with cost $(4 \times 20 + 0) + ((4 + 2) \times 10 + 10) = 150$. All other options are worse than this plan.  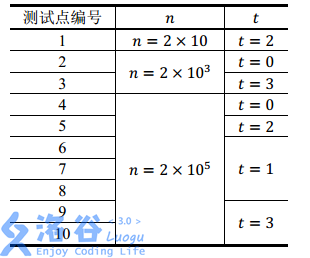Constraints  For all testdata, $n \leq 2 \times 10^5$, $0 \leq p_v \leq 10^6$, $0 \leq q_v \leq 10^{12}$, $1 \leq f_v < v$, $0 < s_v \leq l_v \leq 2 \times 10^{11}$, and the total path length from any city to SZ City does not exceed $2 \times 10^{11}$. The input $t$ denotes the testdata type, $0 \leq t < 4$, where: - When $t = 0$ or $2$, for all cities $v$ in the input, $f_v = v - 1$, i.e., all cities form a chain ending at SZ City. - When $t = 0$ or $1$, for all cities $v$ in the input, $l_v = 2 \times 10^{11}$, i.e., there is no distance limit, and every city can reach all of its ancestors. - When $t = 3$, the testdata has no special property. Translated by ChatGPT 5