P2315 [HNOI2005] Counting Triangles

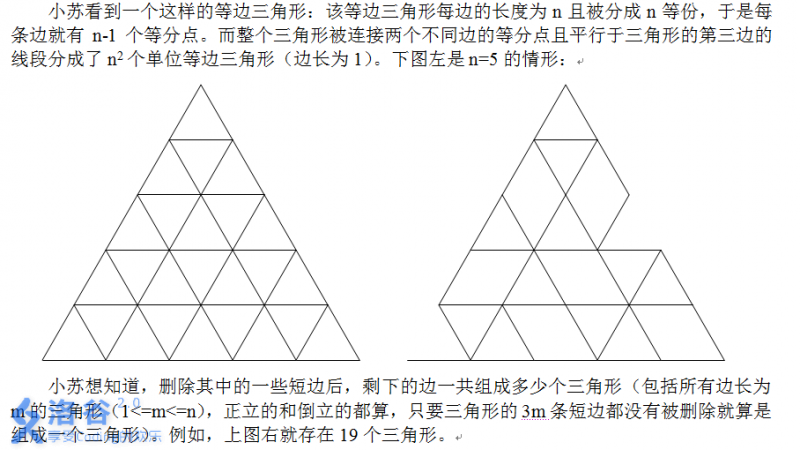
 Xiao Su sees an equilateral triangle: each side of the equilateral triangle has length $n$ and is divided into $n$ equal parts, so each side has $n-1$ division points. The whole triangle is divided into $n^2$ unit equilateral triangles (with side length $1$) by segments that connect division points on two different sides and are parallel to the third side. 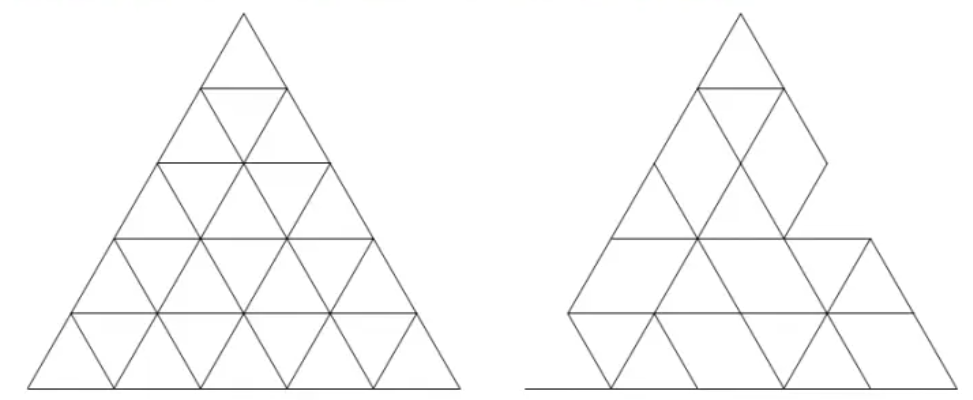The figure on the left below shows the case $n=5$:  Xiao Su wants to know, after deleting some of the short edges, how many triangles are formed by the remaining edges (including all triangles with side length $m$ ($1 \le m < n$), counting both upright and inverted ones). A triangle is counted if all its $3m$ short edges have not been deleted. For example, in the figure on the right above, there are $19$ triangles.

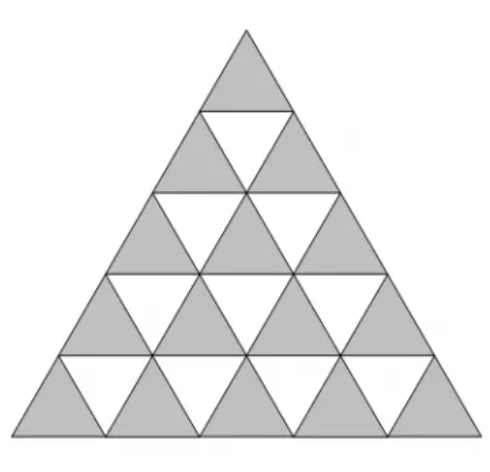
 All short edges of the large triangle can be regarded as the boundaries of $\dfrac{n(n+1)}{2}$ unit triangles, as shown by the gray triangles in the figure below. There is $1$ gray triangle in the $1$st row, $2$ gray triangles in the $2$nd row, …, and $n$ gray triangles in the $n$th row. Therefore, the input format is specified as follows:  The first line contains a positive integer $n$ ($1 \le n \le 1000$), which is the side length of the large triangle. The next $n$ lines: on the $(i+1)$-th line there are $i$ groups of numbers. From left to right, each group describes one triangle. Each group contains $3$ numbers, each either $0$ or $1$, indicating whether the corresponding short edge is deleted. $0$ means deleted, $1$ means not deleted. The three numbers describe, in order, the left, right, and bottom edges of the triangle. Therefore, the $(i+1)$-th line contains $3i$ numbers, each being $0$ or $1$.

Output a single integer $T$, the number of triangles whose boundaries have not been deleted.

Translated by ChatGPT 5