P2315 [HNOI2005] 数三角形

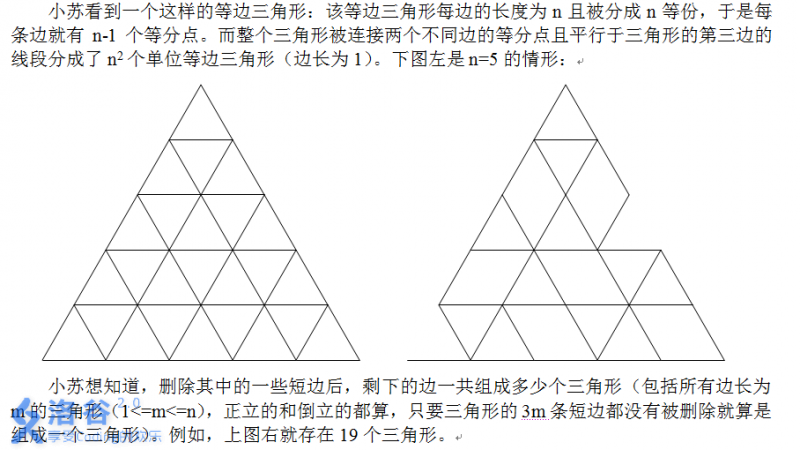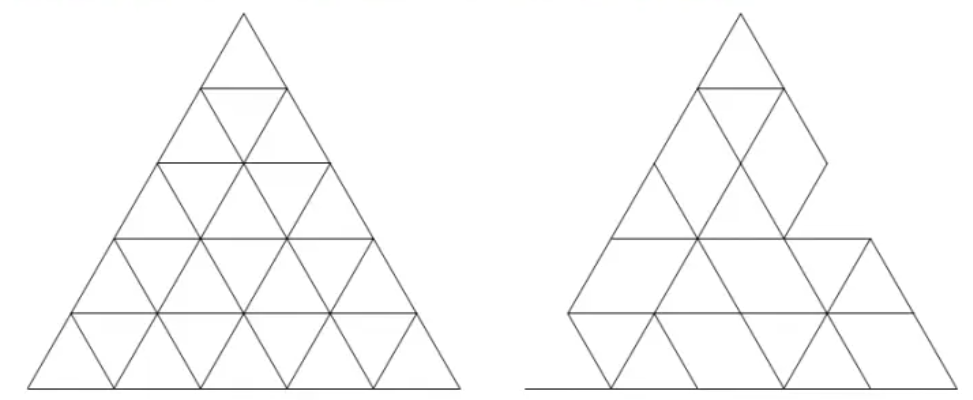
$%$ 小苏看到一个这样的等边三角形：该等边三角形每边的长度为 $ n $ 且被分成 $ n $ 等份，于是每条边就有 $ n-1 $ 个等分点。而整个三角形被连接两个不同边的等分点且平行于三角形的第三边的线段分成了 $ n^2 $ 个单位等边三角形（边长为 $ 1 $）。下图左是 $ n=5 $ 的情形：  小苏想知道，删除其中的一些短边后，剩下的边一共组成多少个三角形（包括所有边长为 $ m $ 的三角形（$ 1 \leq m < n $），正立的和倒立的都算，只要三角形的 $ 3m $ 条短边都没有被删除就算是组成一个三角形）。例如，上图右就存在 $ 19 $ 个三角形。

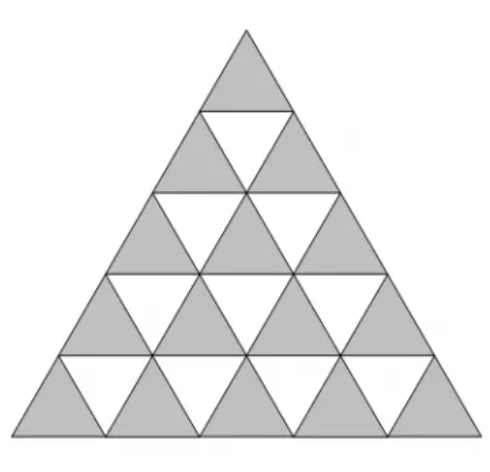
$%$ 大三角形的所有短边可以看成由 $\dfrac{n(n+1)}{2}$ 个单位三角形的边界组成，如下图的灰色三角形所示。其中第 $1$ 排有 $1$ 个灰色三角形，第 $2$ 排有 $2$ 个灰色三角形，……，第 $n$ 排有 $n$ 个灰色三角形。所以输入格式是这样规定的：  第一行为正整数 $n\ (1 \le n \le 1000)$，表示大三角形每边的长度。 接下来的 $n$ 行，第 $i+1$ 行有 $i$ 组数，从左到右每组数描述一个三角形，每组数都有 $3$ 个数，这 $3$ 个数非 $0$ 即 $1$，表示对应的短边是否被删除，$0$ 表示已被删除，$1$ 表示未被删除，依次按照三角形的左、右、下边的顺序来描述。所以第 $i+1$ 行有 $3i$ 个数，每个数是 $0$ 或 $1$。

仅一个整数 $T$，表示有多少个三角形的边界都没有被删除。