P2321 [HNOI2006] Pandora's Box

Legend has it that there is a magical Pandora's box. Whoever opens it will gain happiness, wealth, and love. However, only after truly opening it did people realize that disaster and misfortune come along with it. In fact, when Pandora made this box, she set up some spells to seal away disaster and misfortune. Yet, only in today’s highly advanced scientific age do people have hope of understanding these spells. So for thousands of years, people had no choice but to endure various diseases and the pain of death. However, humanity’s fate has since changed. After decades of research, the NOI organization has finally uncovered the principles behind Pandora’s spells. The spells are produced by a machine called a spell machine. In modern terms, a spell machine is essentially a binary generator. The binary string it generates (this string is called a spell source), once encrypted, becomes a spell. The binary generator has the following structure: It consists of $n$ components, numbered from $0$ to $n - 1$. At any moment, there is exactly one signal, and it stays at some component. A signal is a binary string. Initially, an empty-string signal stays at component $0$. At some moment, if a signal $s$ is staying at component $i$, then component $i$ may append a 0 to the end of the signal and pass it to component $p_{i,0}$, or append a 1 and pass it to component $p_{i,1}$. That is, at the next moment, either a signal S0 (meaning the string S with a 0 appended) stays at component $p_{i,0}$, or a signal S1 stays at component $p_{i,1}$. Some components can output the signal staying on them, and the output signal becomes a spell source. Such components are called spell-source output units. It is not hard to see that some spell sources can be produced by a given spell machine, while others cannot. For example, the spell machine in the figure below can produce spell sources such as 1, 11, 111, 1111, …, but cannot produce 0, 10, 101, etc.  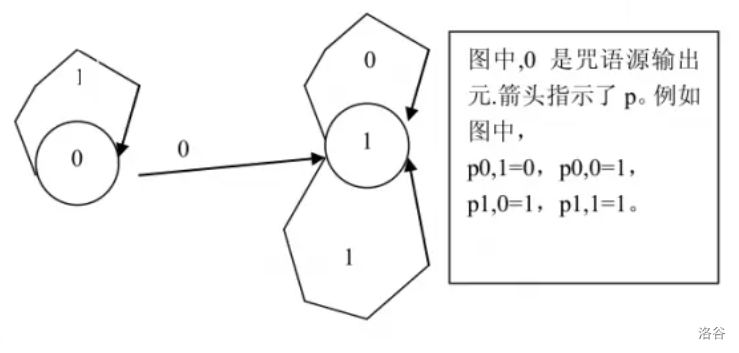On this box, there are $k$ spell machines, labeled from $0$ to $k - 1$. It may happen that every spell source producible by spell machine $i$ can also be produced by spell machine $j$. In that case, we say machine $j$ is an upgrade of machine $i$. One way to measure the complexity of this instance is to consider the maximum number of upgrades of any spell machine on the box. That is, find a longest upgrade sequence $a_1, a_2, \dots, a_t$. This upgrade sequence must satisfy: all machine indices in the sequence are distinct, each is an integer between $0$ and $k - 1$ (inclusive), machine $a_2$ is an upgrade of machine $a_1$, machine $a_3$ is an upgrade of machine $a_2$, …, and machine $a_t$ is an upgrade of machine $a_{t-1}$. Do you want to stay away from disaster and misfortune? Do you want to bask in the sunshine of happiness from now on? Please open your Pandora’s box. But before opening it, you need to compute the longest upgrade sequence on the box.

The first line contains a positive integer $k$ $(1 \le k \le 50)$, the number of spell machines on the box. Then follow $k$ parts, one for each machine: - The first line of each part contains two positive integers $n, m$ $(1 \le n, m \le 50)$, the number of components in this spell machine and the number of spell-source output units, respectively. - The next line contains $m$ integers, the indices of the $m$ spell-source output units. - The next $n$ lines describe transitions. In the $i$-th line, there are two integers $p_{i,0}, p_{i,1}$ between $0$ and $n - 1$ (inclusive).

Output one line with a single integer $t$, the length of the longest upgrade sequence.

For the first sample’s box, there are $4$ spell machines. It is not hard to see that for the $i$-th ($i = 0, 1, 2, 3$) spell machine, all producible spell sources have lengths that are multiples of $(i + 1)$. For the second sample’s box, there are $3$ spell machines: machine $0$ can produce all spell sources; machine $1$ can produce all spell sources whose values, when interpreted as binary, are multiples of $3$; machine $2$ can produce all spell sources whose values, when interpreted as binary, are multiples of $9$. Translated by ChatGPT 5