P2354 [NOI2014] Random Number Generator

Little H is studying randomized algorithms. Randomized algorithms often obtain randomness by calling random number generator functions (for example, random in Pascal and rand in C/C++). In fact, such functions are not truly “random”; they are usually computed by some algorithm. For example, the following quadratic polynomial recurrence is a common algorithm: Choose non-negative integers $x_0, a, b, c, d$ as the random seed, and compute using the following recurrence. For any $i \ge 1$, $x_i = (a \times x_{i-1}^2 + b \times x_{i-1} + c) \mod d$. In this way we can obtain a non-negative integer sequence of arbitrary length $\{ x_i \}, i \ge 1$, and generally we regard this sequence as random. Using the random sequence $\{ x_i \}, i \ge 1$, we can generate a random permutation of $1$ to $K$, denoted $\{ T_i \}, i = 1 \ldots K$, by the following algorithm: 1. Initialize $T$ as the increasing sequence $1$ to $K$. 2. Perform $K$ swaps. At the $i$-th swap, exchange the values of $T_i$ and $T_{(x_i \bmod i) + 1}$. In addition, on top of these $K$ swaps, Little H performs $Q$ extra swap operations. For the $i$-th extra swap, Little H chooses two indices $u_i$ and $v_i$, and swaps the values of $T_{u_i}$ and $T_{v_i}$. To test the practicality of this random permutation generation algorithm, Little H designs the following problem: Little H has a board with $N$ rows and $M$ columns. First, following the above process, after $N \times M + Q$ swap operations, she generates a random permutation of $1 \sim N \times M$, denoted $\{ T_i \}, i = 1 \ldots N \times M$. Then she fills these $N \times M$ numbers into the board row by row and column by column in order: that is, the number filled in the cell at row $i$, column $j$ is $T_{(i - 1) \times M + j}$. Next, Little H wants to start from the top-left corner of the board, i.e., the cell at row $1$, column $1$. Each move goes either right or down, and without leaving the board, she reaches the bottom-right corner, i.e., the cell at row $N$, column $M$. Little H records the numbers on all visited cells, and sorts them in ascending order. Thus, for any valid path, Little H can obtain an increasing sequence of length $N + M - 1$, which we call the path sequence. Little H wants to know what the lexicographically smallest path sequence she can obtain is.

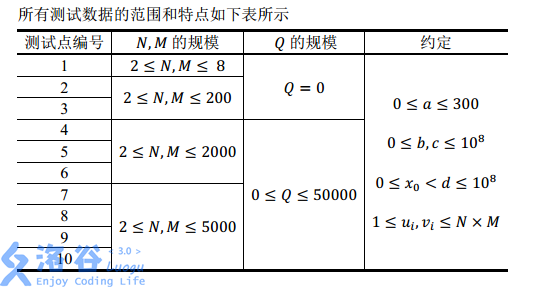
The first line contains $5$ integers $x_0, a, b, c, d$, describing the random seed required by Little H’s random number generation algorithm. The second line contains three integers $N, M, Q$, indicating that Little H wants to generate a permutation of $1$ to $N \times M$ to fill her $N$-row $M$-column board, and that after the initial $N \times M$ swap operations, she performs $Q$ extra swap operations. The next $Q$ lines each contain two integers $u_i, v_i$, indicating that at the $i$-th extra swap operation, the values of $T_{u_i}$ and $T_{v_i}$ are swapped.

Output one line containing $N + M - 1$ positive integers separated by spaces, representing the lexicographically smallest path sequence that can be obtained.

For Sample 1, according to the input seeds, the first $12$ random numbers $x_i$ that Little H obtains are: 9 5 30 11 64 42 36 22 1 9 5 30 Based on these $12$ random numbers, after the initial $12$ swap operations, Little H obtains the permutation: 6 9 1 4 5 11 12 2 7 10 3 8 After the additional $3$ swap operations, Little H obtains the final random permutation: 12 9 1 7 5 11 6 2 4 10 3 8 ```cpp 12 9 1 7 5 11 6 2 4 10 3 8 ``` The optimal path passes through the numbers: 12-9-1-6-2-8.  Translated by ChatGPT 5