P2377 Triangle Graph

Please view the original statement [here](https://www.luogu.com.cn/paste/tre46v8i).

UNowen has $n$ [plane vectors](https://baike.baidu.com/item/%E5%B9%B3%E9%9D%A2%E5%90%91%E9%87%8F/448934?fr=ge_ala) $\{\bm L_n\}$, where: - $|\bm L_1|=|\bm L_2|=\ldots=|\bm L_n|=1$; - $\bm L_1+\bm L_2+\ldots+\bm L_n=\bm 0$; - For any positive integers $1 \le i,j \le n$, there always exists an integer $k$ such that $\langle\bm L_i,\bm L_j\rangle=\dfrac{k\pi}{3}$; ([$\dfrac{k\pi}{3}=k \times 60^\circ$](https://baike.baidu.com/item/%E5%BC%A7%E5%BA%A6/1533188?fr=ge_ala)) - Except for the entire vector sequence (same below), there is no contiguous subsequence in the vector sequence whose sum is $\bm 0$. Here $\langle\bm X,\bm Y\rangle$ denotes “the angle by which $\bm X$ is rotated to point in the same direction as $\bm Y$,” where counterclockwise is positive and clockwise is negative (for example, let $\bm X=(\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2})$, $\bm Y=(1,0)$, then $\langle\bm X,\bm Y\rangle=-\dfrac{\pi}{4}$). In other words, all $n$ vectors have length $1$, and concatenating them head to tail forms a closed polygon. It is guaranteed that each interior angle of this polygon is an integer multiple of $\dfrac{\pi}{3}$, its interior contains no other vectors, and it is not hollow. For convenience, we use a string $S$ of length $n$ over the alphabet $\{\tt a,\tt b,\tt c,\tt d,\tt e,\#\}$ to describe $\{\bm L_n\}$. Specifically, for the $i$-th character in $S$ (in particular, $\bm L_0$ is equivalent to $\bm L_n$, and $\bm L_{n+1}$ is equivalent to $\bm L_1$, similarly below): | 字符 | 含义 | | :----------: | :----------: | | $\tt a$ | $\langle\bm L_i,\bm L_{i+1}\rangle=\dfrac{2\pi}{3}$ | | $\tt b$ | $\langle\bm L_i,\bm L_{i+1}\rangle=\dfrac{\pi}{3}$ | | $\tt c$ | $\langle\bm L_i,\bm L_{i+1}\rangle=0$ | | $\tt d$ | $\langle\bm L_i,\bm L_{i+1}\rangle=-\dfrac{\pi}{3}$ | | $\tt e$ | $\langle\bm L_i,\bm L_{i+1}\rangle=-\dfrac{2\pi}{3}$ | | $\tt \#$ | $\vert\langle\bm L_i,\bm L_{i+1}\rangle\vert=\pi$ |  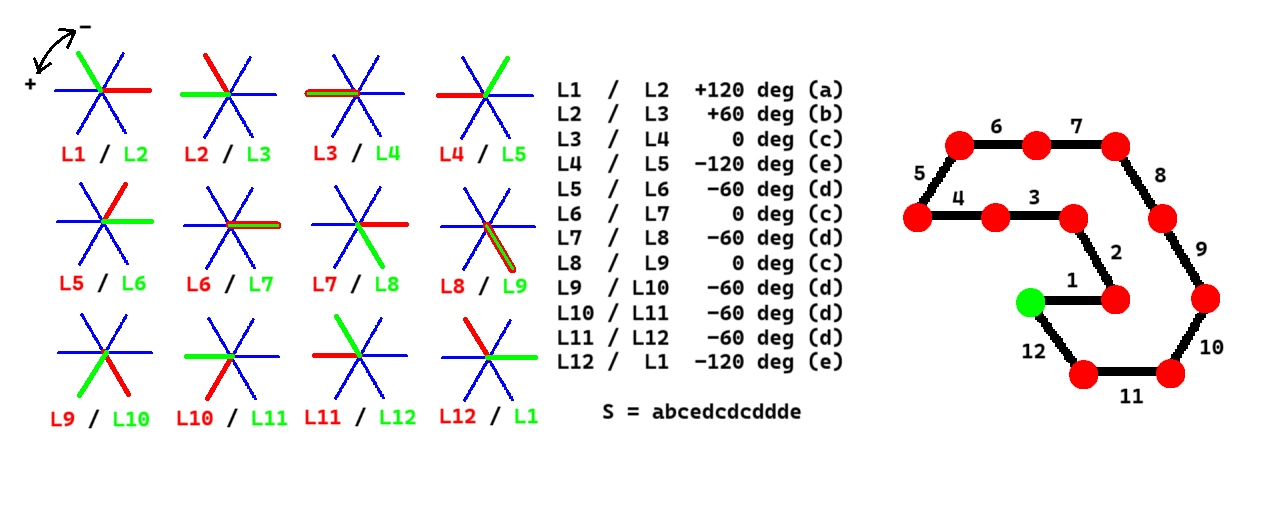In addition, UNowen defines a “standard representation” of a vector sequence $\{\bm L_1,\bm L_2,\ldots,\bm L_n\}$ as follows: - For $l=1,2,\ldots,n$, compute the string corresponding to the vector sequence $\{\bm L_l,\bm L_{l+1},\ldots,\bm L_n,\bm L_1,\bm L_2,\ldots,\bm L_{l-1}\}$. - Among these $n$ strings, take the lexicographically smallest string as the “standard representation” of the vector sequence $\{\bm L_1,\bm L_2,\ldots,\bm L_n\}$. For example, the “standard representation” of the vector sequence in the figure above is $S=\texttt{abcedcdcddde}$, and not $S=\texttt{dcdcdddeabce}$. Now, UNowen gives you the string $S$ corresponding to the vector sequence $\{\bm L_1,\bm L_2,\ldots,\bm L_n\}$ (which is not necessarily its “standard representation”). He hopes you can perform one modification to this vector sequence as follows: - Choose a positive integer $1 \le k \le n$. - Construct two plane vectors $\bm X,\bm Y$ such that: - $|\bm X|=1$; - $|\bm Y|=1$; - $\langle\bm L_k,\bm X\rangle=\dfrac{\pi}{3}$; - $\langle\bm L_k,\bm Y\rangle=-\dfrac{\pi}{3}$. - Replace $\bm L_k$ with two items $\bm X,\bm Y$ (with $\bm X$ before $\bm Y$). - If $\bm L_{k-1}+\bm X=\bm 0$, delete $\bm L_{k-1}$ and $\bm X$. - If $\bm L_{k+1}+\bm Y=\bm 0$, delete $\bm L_{k+1}$ and $\bm Y$. - If after the modification there exists a contiguous subsequence whose sum is $\bm 0$ (other than the entire vector sequence), then UNowen considers this modification invalid. For example, in the figure below, if you choose $k=3$, then the modification is invalid. - UNowen defines the “modification result” as the “standard representation” of the modified vector sequence. - For any two modification schemes, if the polygons obtained by concatenating the modified vector sequences head to tail are congruent, then UNowen considers the two modification schemes equivalent. For example, in the figure below, the two modification schemes $k=1$ and $k=2$ are equivalent. - That is, the modification operation constructs an outward equilateral triangle on some vector of the closed polygon, such that the modified shape is still a closed polygon satisfying the above requirements (each interior angle is an integer multiple of $\dfrac{\pi}{3}$, the interior contains no other vectors, and it is not hollow). For any two modification schemes, if the polygons obtained from the modified sequences are congruent, then they are equivalent.  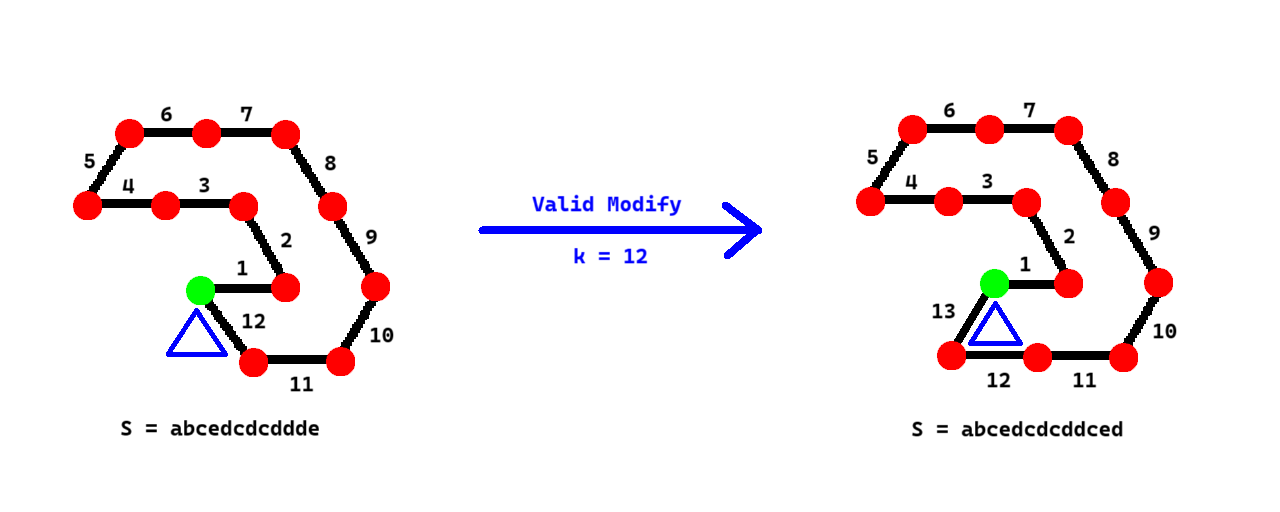Find the number of pairwise non-equivalent valid modification schemes, and output the “modification result” of each scheme in lexicographic order.

This problem contains multiple test cases. The first line contains a positive integer $T$, the number of test cases. The next $T$ lines each contain a non-empty string $S$ over the alphabet $\{\tt a,\tt b,\tt c,\tt d,\tt e\}$. It is guaranteed that $\tt \#$ will not appear.

For each test case, output three lines: - The first line contains a positive integer $K$, the number of pairwise non-equivalent valid modification schemes. - The second line contains $K$ non-empty strings over the alphabet $\{\tt a,\tt b,\tt c,\tt d,\tt e\}$ (separated by spaces), representing each possible “modification result.” You must output them in lexicographic order. It can be proven that $\tt \#$ will not appear. - The third line is an empty line. Please pay special attention to this, as it does not follow the usual data format of traditional problems.

Let $|S|$ be the length of the string $S$. - For $30\%$ of the testdata, $T \le 5$, $|S| \le 9$. - For $50\%$ of the testdata, it is guaranteed that all modification schemes are valid. - For $100\%$ of the testdata, $1 \le T \le 100$, $3 \le |S| \le 75$. Translated by ChatGPT 5