P2403 [SDOI2010] The Treasure of the King of Sotomon

In the vast African desert lives a hardworking and brave alpaca clan. AlpacaL.Sotomon, respectfully called the “Prophet” by his people, is the leader of the clan and is known to outsiders as the “King of Sotomon.” He devoted his life to maintaining the clan’s peace and harmony, and once personally led his army to crush the savage invasion of the River Crab imperialists, earning great merit. The King of Sotomon amassed countless treasures in his lifetime, but being frugal and low-key by nature, he buried them in an underground palace of his own design. This is where the story of Henry Curtis begins. Henry is a greedy yet shrewd man who meticulously planned this heist and, after overcoming numerous traps, arrived at the entrance of the underground palace. The palace is arranged in a matrix of $R \times C$ rectangular chambers. Treasures are buried in $N$ of these chambers, which are called treasure chambers. The palace is enclosed by solid walls, and adjacent chambers are separated by walls as well. One can move from one chamber to another only through a unique transportation method invented by the King of Sotomon: teleportation gates. Each of the $N$ treasure chambers is equipped with exactly one teleportation gate; chambers without treasures have no gates. All gates fall into one of three types: 1. “Horizontal Gate”: from this gate, one can teleport to any chamber in the same row. 2. “Vertical Gate”: from this gate, one can teleport to any chamber in the same column. 3. “Any Gate”: from this gate, one can teleport to any of the 8 neighboring chambers around the current chamber (if the target chamber exists). Being far-sighted, Henry had already obtained the palace’s original construction tender book, which records in detail the location and type of every teleportation gate. Although the palace is sealed from the outside, Henry has prepared a portable gate that can teleport him into any chamber to start his search and can teleport him out from any chamber after he finishes. He may enter the palace once and exit once in total, and the portable gate cannot be used to move between chambers. Fortunately, in-palace teleportation gates can be used without limit, and any chamber may be entered and left multiple times. Now that Henry has opened his portable gate and is about to choose a chamber to enter, he wants to plan a route that visits as many distinct treasure chambers as possible. Please tell Henry the maximum number of distinct treasure chambers that such a route can visit.

The first line contains three positive integers $N, R, C$. Each of the following $N$ lines describes a teleportation gate with three positive integers $x_i, y_i, T_i$, meaning there is a gate in the treasure chamber at row $x_i$, column $y_i$, and its type is $T_i$. $T_i$ is an integer between $1$ and $3$: $1$ means a “Horizontal Gate” that can teleport to any column in row $x_i$, $2$ means a “Vertical Gate” that can teleport to any row in column $y_i$, and $3$ means an “Any Gate” that can teleport to any of the 8 neighboring chambers. It is guaranteed that $1 \le x_i \le R$, $1 \le y_i \le C$, and all gate positions are distinct.

Output a single positive integer: the maximum number of distinct treasure chambers that your determined route can visit.

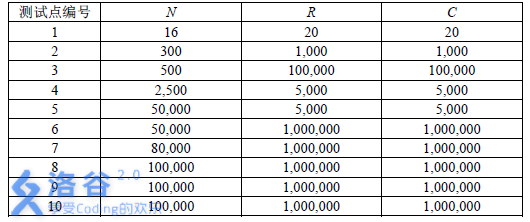
Constraints and Conventions:  Translated by ChatGPT 5