P2421 [NOI2002] Savages on a Desert Island

The island of Crete is known for its tribes of savages. There are $m$ caves arranged in a ring on the island. These caves are numbered clockwise as $1, 2, \dots, m$. There are $n$ savages living on the island, initially residing in caves $C_1, C_2, \dots, C_n$ in order. Afterward, each year, the $i$-th savage moves forward clockwise by $P_i$ caves and settles there. Each savage $i$ has a lifespan value $L_i$, i.e., the number of years they live. The following four figures describe the first four years on an island with $6$ caves and three savages. The initial cave numbers of the three savages are $1, 2, 3$; the number of caves they move each year are $3, 7, 2$; and their lifespan values are $4, 3, 1$.  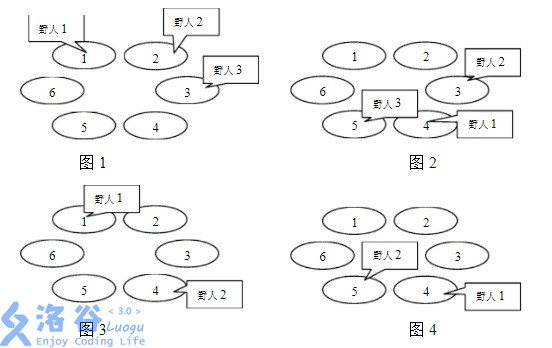Strangely, although there are many savages, no two savages ever occupy the same cave during their lifetimes, so the island remains peaceful and tranquil. Scientists are curious: what is the minimum number of caves needed to maintain peace on the island?

The first line contains an integer $n$ ($1 \leq n \leq 15$), the number of savages. Lines $2$ to $n+1$ each contain three integers $C_i, P_i, L_i$ ($1 \leq C_i, P_i \leq 100$, $0 \leq L_i \leq 10^6$), representing the initial cave number, the number of caves moved each year, and the lifespan value for each savage.

Output a single number $M$, the minimum possible number of caves. It is guaranteed that the input has a solution and $M \leq 10^6$.

$1 \leq n \leq 15$, $1 \leq C_i, P_i \leq 100$, $0 \leq L_i \leq 10^6$. It is guaranteed that $M \leq 10^6$. Translated by ChatGPT 5