P2446 [SDOI2010] Mainland Conquest

In a distant world, there are two countries: Jason, located at the western end of the continent, and Chris, located at the eastern end. The two peoples believe in two opposing gods: Jason worships Zeng · Blazer, the god symbolizing darkness and destruction, while Chris worships Spring · Blazer, the god symbolizing light and eternity. In Fantasia Year $8012$ January, Jason officially declared Zeng · Blazer as their only god, and began persecuting Chris believers of Spring · Blazer within Jason. On Fantasia Year $8012$ March $2$, the Chris believers in Shenyu Town, a small town in eastern Jason, launched an uprising. On Fantasia Year $8012$ March $7$, the uprising in Shenyu Town was brutally suppressed by Jason’s army. On Fantasia Year $8012$ March $8$, Chris declared war on Jason. The Chris legions, hundreds of thousands strong, marched to the border between the two countries and faced off against Jason’s legions. In Fantasia Year $8012$ April, the Chris legions broke through Jason’s defensive line and entered Shenyu Town, freeing the surviving Chris believers there. The war then entered a stalemate and dragged on. The fighting was brutal, with gunfire and smoke everywhere, leaving the people in misery.

On Fantasia Year $8012$ May $12$ late at night, Spring · Blazer delivered an oracle: “Trust me, earn eternal life.” The morale of the Chris legions soared. As the commander-in-chief of the Chris legions, you decide to seize this opportunity to launch a surprise attack and defeat Jason in one stroke. Specifically, Jason has $N$ cities connected by $M$ directed roads. Shenyu Town is city $1$, and Jason’s capital is city $N$. You only need to destroy the Great Temple of Zeng · Blazer located in the capital of Jason; once it falls, Jason’s faith, army, and everything else will collapse and vanish. To minimize your own losses, you decide to use self-destruct robots to accomplish this task. The only difficulty is that some cities in Jason are protected by barriers. You cannot enter a city without first disabling its barrier. Each city’s barrier is maintained by several barrier generators distributed in other cities. If you want to enter a city, you must destroy all the barrier generators that maintain that city’s barrier. You have an unlimited number of self-destruct robots. Once a robot enters a city, it can detonate instantly to destroy a single target (either a barrier generator or the Great Temple), and of course the robot itself is also destroyed. You need to find the minimum time required to bring down Jason. It is guaranteed that there is always a solution. No barrier generator that maintains a city’s barrier is located inside that very city. There may be multiple roads between the same pair of cities, and self-loops may exist.

The first line contains two positive integers $N, M$. The next $M$ lines each contain three positive integers $u_i, v_i, w_i$, indicating there is a directed road from city $u_i$ to city $v_i$, and a self-destruct robot needs $w_i$ time to traverse this road. Then follow $N$ lines, each describing one city. Each line starts with a positive integer $l_i$, the number of barrier generators maintaining this city’s barrier, followed by $l_i$ city indices between $1 \ldots N$ indicating the locations of those generators. If $l_i = 0$, then this city has no barrier. It is guaranteed that $l_1 = 0$.

Output a single positive integer: the minimum time required to defeat Jason.

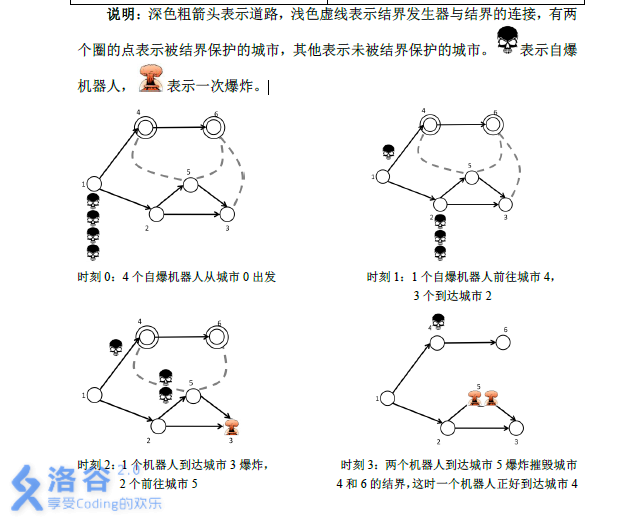
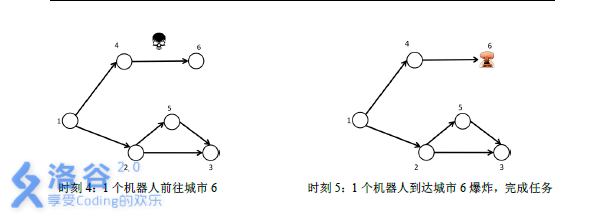
  Constraints: - For $20\%$ of the testdata, $N \le 15$, $M \le 50$. - For $50\%$ of the testdata, $N \le 500$, $M \le 6 \times 10^3$. - For $100\%$ of the testdata, $1 \le N \le 3 \times 10^3$, $1 \le M \le 7 \times 10^4$, $1 \le w_i \le 10^8$. Translated by ChatGPT 5