P2449 [SDOI2005] 矩形
题目描述
现在我们在一个平面上画了 $n$ 个矩形。每一个矩形的两边都与坐标轴相平行,且矩形定点的坐标均为整数。现我们定义满足如下性质的图形为一个块:
1. 每一个矩形都是一个块;
2. 如果两个块有一段公共的部分,那么这两个块就会形成一个新的块,否则这两个块就是不同的。
示例:
图 $1$ 中的矩形形成了两个不同的块。图 $2$ 中的矩形形成了一个块。
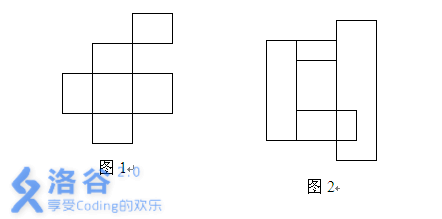
任务:
请写一个程序:
1. 从文本文件 `PRO.IN` 中读入各个矩形的顶点坐标;
2. 找出这些矩形中不同的块的数目;
3. 把结果输出到文本文件 `PRO.OUT` 中。
输入格式
输入的第一行包括一个整数 $n$,$1\le n\le 7000$ 为矩形的数目。以下的 $n$ 行为矩形顶点的坐标。每一个矩形都是用四个整数来描述的:左下角的 $x$ 坐标、左下角的 $y$ 坐标、右上角的 $x$ 坐标和右上角的 $y$ 坐标。所有的坐标都是不大于 $10000$ 的非负整数。
输出格式
输出唯一的一个整数——这些矩形所形成的不同的块的数目。
说明/提示
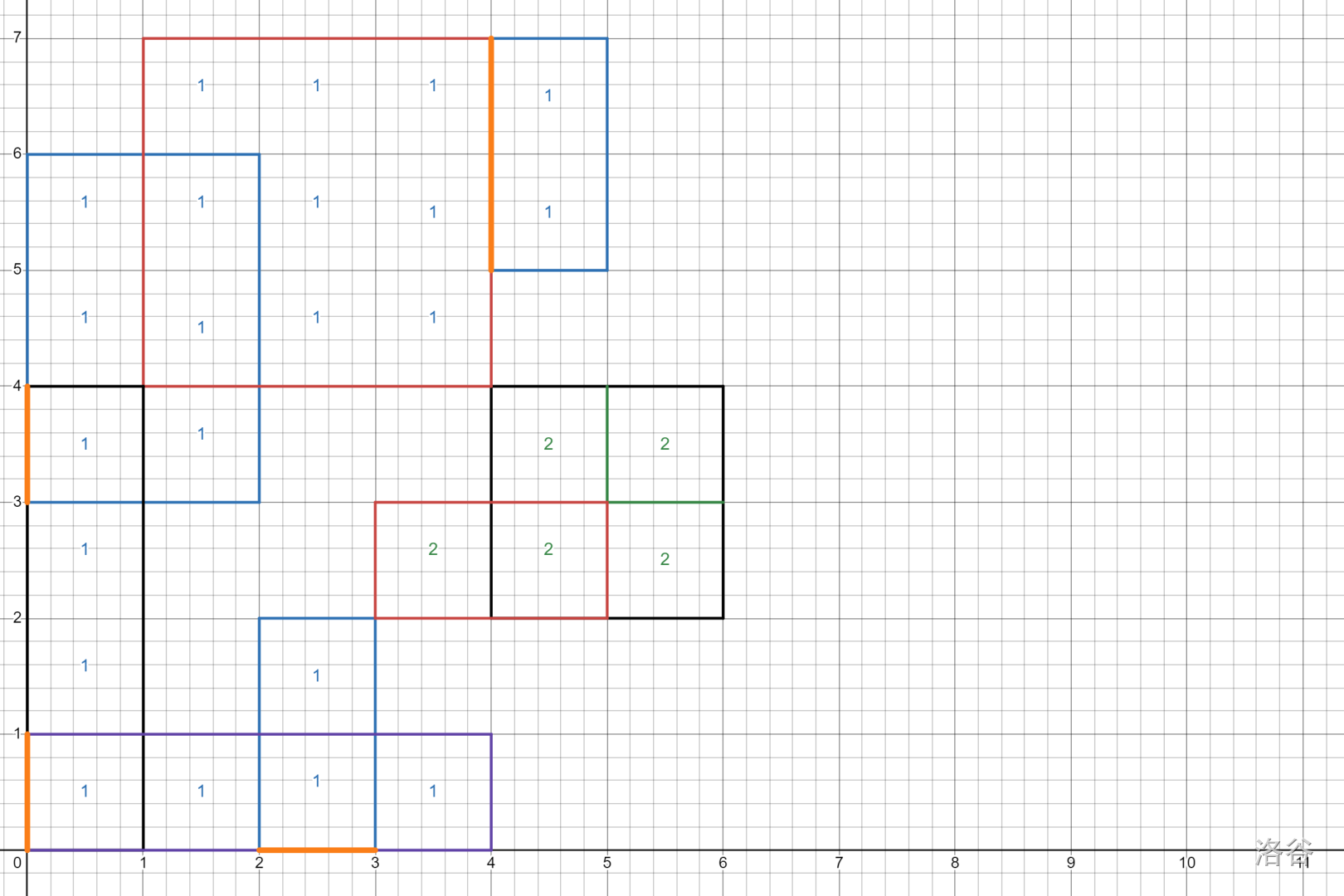
[图片链接](https://www.desmos.com/calculator/1g1ohcqqex)
橙色加粗的线段表示这里有重合的部分,每一个方形中间的数字表示所属的块的编号。
注意:角重合不算同一个块。