P2459 [SDOI2007] 3D Partition

Ghy recruited $n$ underlings, such as Psf, Hf, Csr, Ll, and of course you. (as in the original text...) As the boss, he never asks his underlings for anything. Instead, he often gives them gifts. One day, he got a rectangular cuboid cake. But Ghy does not like eating cake, so he wants to give all of it to his underlings. Ghy believes all underlings are equal, so he asks you to divide this cake into $n$ rectangular cuboid small cakes that are equal in both size and shape (i.e., congruent small cakes). We move the cake into a 3D coordinate system, taking one vertex $O$ as the origin $ (0, 0, 0) $. The vertex opposite to $O$ (the farthest point from $O$) has coordinates $ (x, y, z) $. In fact, $ x, y, z $ represent the length, width, and height of the rectangular cuboid.

Four positive integers, $ x, y, z, n $. Their meanings are as described above.

$n$ lines, each containing 6 real numbers, representing the coordinates of a pair of opposite vertices of one congruent rectangular cuboid small cake. Output the coordinates of the first vertex $x_1, y_1, z_1$, followed by $x_2, y_2, z_2$. The absolute error must not exceed $10^{-9}$. You may output the small cakes in any order, and for each small cake, you may output any one pair of opposite vertices.

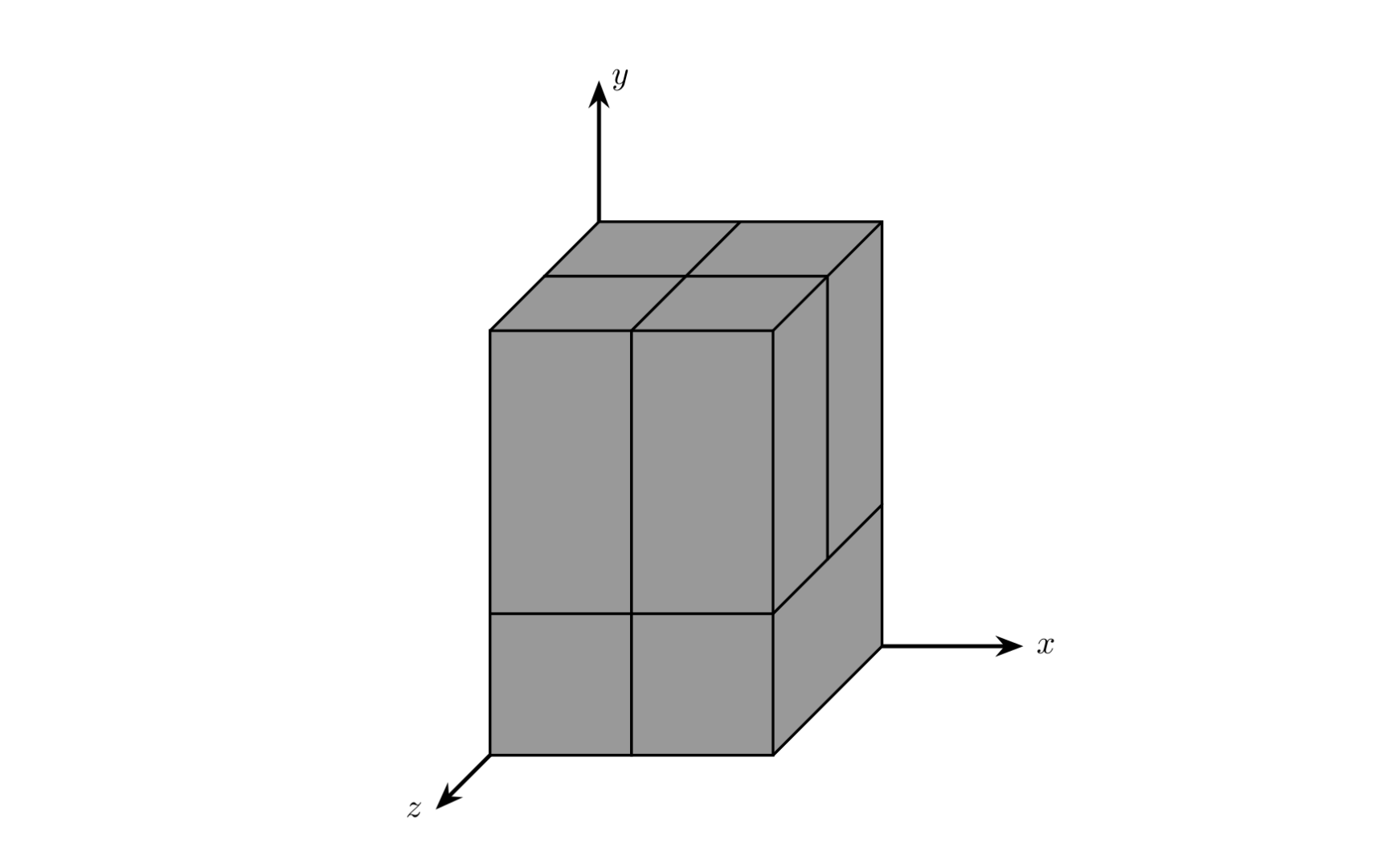
Sample explanation (added by admin on 2023-09-29).  Constraints For $100\%$ of the testdata, $1 \leq x, y, z, n \leq 1000$, and $x, y, z$ are integers. Translated by ChatGPT 5