P2467 [SDOI2010] Goblin Tribe

Legend has it that a long time ago, there lived a mysterious creature on the earth: the goblin. Goblins like to live in continuous mountain ranges. Specifically, a mountain range $h$ of length $n$ can be divided from left to right into $n$ segments, each with a unique height $h_i$, where $h_i$ is a positive integer between $1$ and $n$. If a segment is higher than all of its adjacent segments, then this segment is a peak. A segment at the edge has only one adjacent segment; all others have two (i.e., one on the left and one on the right). Similarly, if a segment is lower than all of its adjacent segments, then this segment is a valley. Goblins share a hobby—drinking, and taverns can be set up in valleys. Goblin taverns are always bustling day and night, and the aroma of goblin wine can spread for miles. Goblins are also highly alert. They can set up watchtowers on every peak and take turns on watch to ensure they learn of any invasion at the first moment. The goblins hope that each of the $n$ segments can have either a watchtower or a tavern. Only a mountain range that satisfies this condition could be inhabited by goblins. Now you want to know how many mountain ranges of length $n$ could possibly be inhabited by goblins. Two mountain ranges $a$ and $b$ are different if and only if there exists an $i$ such that $a_i \ne b_i$. Since this number can be large, you are only interested in its remainder modulo $p$.

One line with two positive integers $n, p$.

A non-negative integer, the result of the required answer modulo $p$.

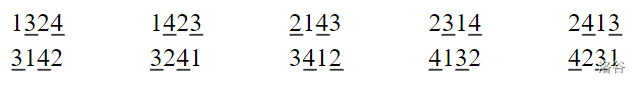
There are $10$ possible mountain ranges, which are:  The marked numbers indicate peaks where watchtowers can be set up; the others indicate valleys where taverns can be set up. Constraints - For $20\%$ of the testdata, $N \le 10$. - For $40\%$ of the testdata, $N \le 18$. - For $70\%$ of the testdata, $N \le 550$. - For $100\%$ of the testdata, $3 \le N \le 4200$, $P \le 10^9$. Translated by ChatGPT 5