P2481 [SDOI2010] Code Auction

As iPig’s mastery of the P++ language grows, he has built his own complete code library. Students in the Pig Kingdom who want to participate in POI are all scrambling to ask iPig for the library. iPig does not want to give the code library to every piglet who wants it; he only wants to give it to some piglets who are both close to him and willing to pay, so he decides to hold a huge auction. At the auction, all $N$ piglets will stand in a line from left to right, ordered by their favorability with iPig from low to high. Each piglet has $9$ pig-coins (exchange rate with RMB unknown). Starting from the left, each piglet in turn raises a sign showing an integer from $1$ to $9$, indicating how many pig-coins they want to pay for the code library. Everyone knows that if they bid less than the pig on their left, they will certainly not get the coveted code library; therefore, starting from the second pig, each bid is greater than or equal to the bid of the pig on the left. The piglet(s) who bid the most in the end will receive iPig’s code library and move toward the dream of being recommended to PKU (Pig Kingdom University). iPig is very pleased with this idea. On the way to the venue, he starts imagining the scenes at the auction, such as how many different bidding sequences there will be, but these questions are too easy and no longer interest him. He wants to study a harder problem. iPig notices that if he looks down from the stage, the signs raised by the pigs from left to right form exactly an $N$-digit integer. He now wants to tackle the following problem: among all possible integers that can be formed, how many are exactly divisible by $P$? Since the answer can be large, he only wants the answer $\bmod\ 999911659$.

There is exactly one line containing two numbers $N\ (1 \le N \le 10^{18})$ and $P\ (1 \le P \le 500)$, separated by a space.

Output exactly one line containing a single number, the remainder when the answer is divided by $999911659$.

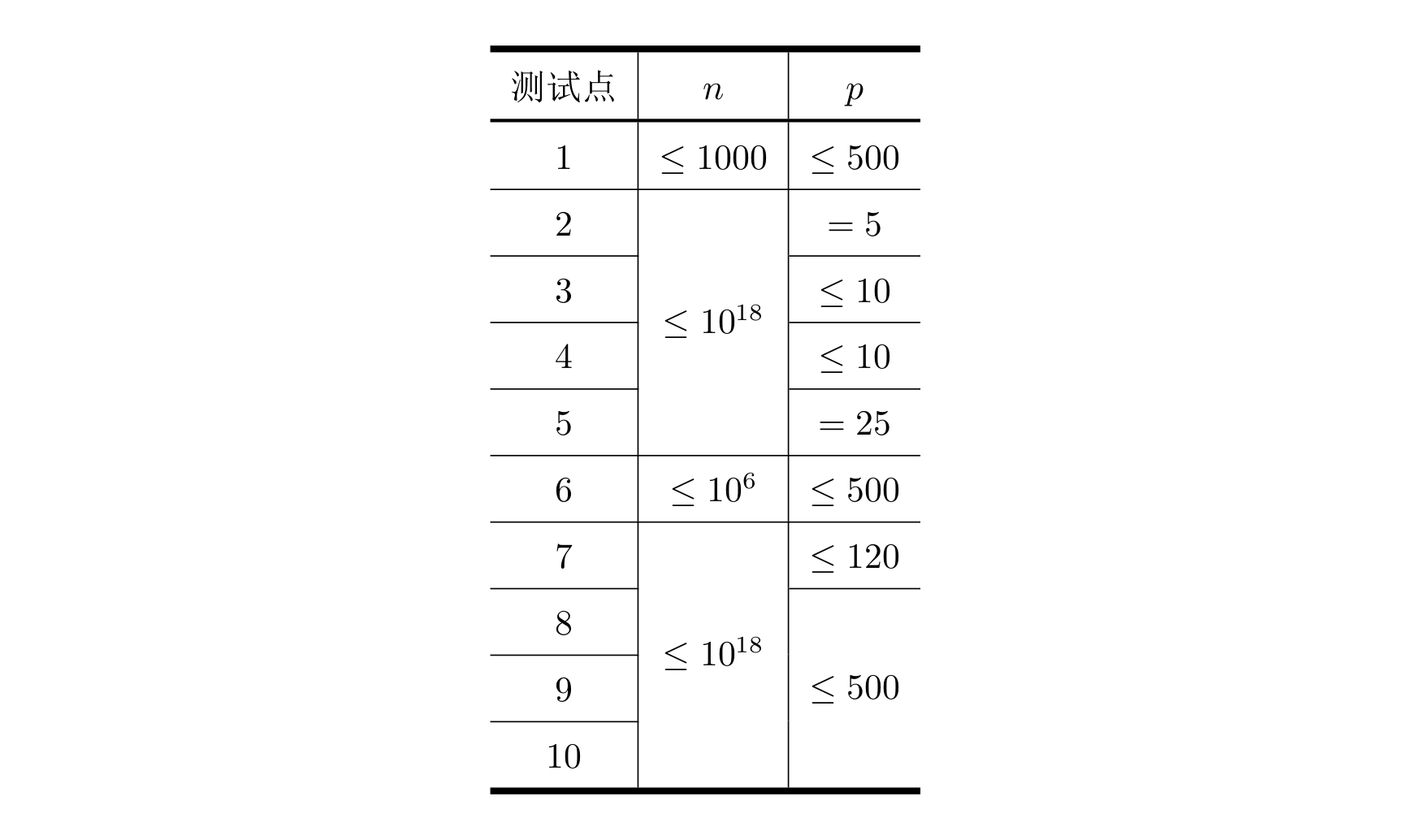
### Sample Explanation The valid sequences can be: $12,\allowbreak 15,\allowbreak 18,\allowbreak 24,\allowbreak 27,\allowbreak 33,\allowbreak 36,\allowbreak 39,\allowbreak 45,\allowbreak 48,\allowbreak 57,\allowbreak 66,\allowbreak 69,\allowbreak 78,\allowbreak 99$, for a total of $15$. ### Constraints  Translated by ChatGPT 5