P2540 [NOIP 2015 提高组] 斗地主 加强版

牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的 $A$ 到 $K$ 加上大小王的共 $54$ 张牌来进行的扑克牌游戏。在斗地主中，牌的大小关系根据牌的数码表示如下：$3

第一行包含用空格隔开的 $2$ 个正整数 $T,n$，表示手牌的组数以及每组手牌的张数。 接下来 $T$ 组数据，每组数据 $n$ 行，每行一个非负整数对 $a_i,b_i$，表示一张牌，其中 $a_i$ 表示牌的数码，$b_i$ 表示牌的花色，中间用空格隔开。特别的，我们用 $1$ 来表示数码 $A$，$11$ 表示数码 $J$，$12$ 表示数码 $Q$，$13$ 表示数码 $K$；黑桃、红心、梅花、方片分别用 $1-4$ 来表示；小王的表示方法为 `0 1`，大王的表示方法为 `0 2`。

共 $T$ 行，每行一个整数，表示打光第 $i$ 手牌的最少次数。

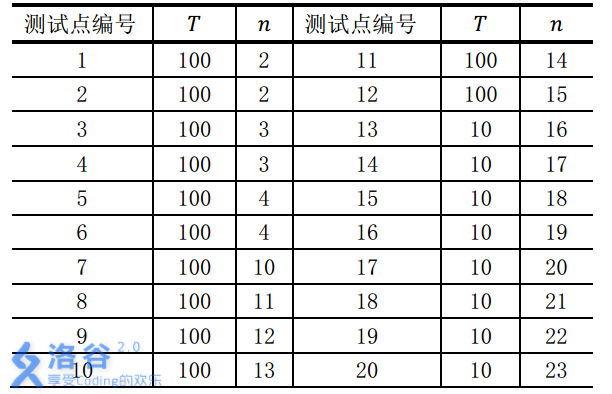
#### 样例 1 说明 共有 $1$ 组手牌，包含 $8$ 张牌：方片 $7$，方片 $8$，黑桃 $9$，方片 $10$，黑桃 $J$，黑桃 $5$，方片 $A$ 以及黑桃 $A$。可以通过打单顺子（方片 $7$，方片 $8$，黑桃 $9$，方片 $10$，黑桃 $J$），单张牌（黑桃 $5$）以及对子牌（黑桃 $A$ 以及方片 $A$）在 $3$ 次内打光。 #### 数据范围与提示 对于前 $20$ 个测试点， 我们约定手牌组数 $T$ 与张数 $n$ 的规模如下：  数据不保证所有的手牌都是随机生成的。