P2542 [AHOI2005] Route Planning

Exploration of planet Samuel has achieved great success, so scientists turned their attention to the galaxy where planet Samuel resides—a vast Samuel Galaxy composed of hundreds of millions of planets. After long-term probing, the Samuel II supercomputer of the interstellar space station has located the spatial coordinates of $n$ planets in the Samuel Galaxy and numbered these planets from $1$ to $n$. Some advance spacecraft have set out and opened exploration routes between planets. Exploration routes are bidirectional. For example, if an exploration route is opened from planet $1$ to planet $3$, then the route can also be used from planet $3$ to planet $1$. 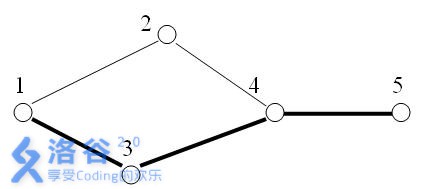For example, see the figure below:  Among $5$ planets, there are $5$ exploration routes. For two planets $A$ and $B$, if removing a certain route makes it impossible to travel from planet $A$ to planet $B$, we call that route a critical route. Obviously, in the figure above, there is $1$ critical route between planets $1$ and $5$: that is, the $4 \leftrightarrow 5$ route. However, due to unknown magnetic storms and planetary collisions in the universe, some existing routes are damaged. As more and more routes are destroyed and exploration ships cannot repair them in time, the number of critical routes between two planets will increase. Suppose in the figure above, the route $4 \leftrightarrow 2$ (from planet $4$ to planet $2$) is destroyed. At this time, there are $3$ critical routes between planets $1$ and $5$: $1 \leftrightarrow 3$, $3 \leftrightarrow 4$, and $4 \leftrightarrow 5$. Xiao Lian’s task is to continuously monitor route destructions and report, at any time, the number of critical routes between two planets. Please help complete this task.

The first line contains two integers, representing the number of planets $n$ and the initial number of routes $m$. The next $m$ lines each contain two distinct integers $u, v$, indicating that there is a route between planet $u$ and planet $v$. Then follow several lines. Each line first gives an integer $op$, indicating the type of an operation. - If $op = 1$, then two integers $u, v$ follow, asking how many critical routes currently exist between planets $u$ and $v$. - If $op = 0$, then two integers $u, v$ follow, indicating that the route between $u$ and $v$ is destroyed. - If $op = -1$, the input ends and no further operations follow.

For each query with $op = 1$, output one integer on a separate line indicating the number of critical routes.

Constraints and Conventions - $1 \leq n \leq 3 \times 10^4$, $1 \leq m \leq 10^5$. - $-1 \leq op \leq 1$, $1 \leq u, v \leq n$. - Regardless of how routes are destroyed, at any time any two planets can reach each other. In the entire testdata, between any two planets there is at most one direct route. - For operations with $op = 0$, it is guaranteed that the route $u \leftrightarrow v$ exists before the operation. - The total number of queries and route destructions does not exceed $4 \times 10^4$. Update: 2025.6.27 Added one set of testdata. Translated by ChatGPT 5