P2545 [AHOI2004] Experimental Base

After unremitting efforts, scientists in our country are officially launching the research program for planet Samuel. The current task is to transport intelligent robots to the planet by spacecraft to establish a temporary experimental base for in-depth scientific exploration. To inspire students’ interest in science, scientists have also set up Student Research Teams (SRT) worldwide. After multiple rounds of selection, Xiao Keke has finally been admitted to the team. Senior scientists assigned Xiao Keke a simple operations task: In the preliminary orbital survey of planet Samuel, it was found that the planet has several narrow flat regions suitable for landing (also called “landing zones”). Scientists plan to build an experimental base in a landing zone. However, not every landing zone is suitable for construction. To this end, each landing zone has been divided into $2 \times N$ rectangles. Different landing zones have different values of $N$. During the survey, the suitability of each rectangular plot was assessed. For example, the suitability values for a $2 \times 9$ landing zone are shown below:  Among these rectangular plots, those with positive suitability are firm and flat, suitable for building the base; the higher the positive value, the safer and more suitable it is. Some plots have negative suitability, indicating danger; the more negative it is, the less suitable it is for construction. Scientists wish to choose a $2 \times Q$ segment within a landing zone to build the experimental base. For convenience in research, it is required that within the $2 \times Q$ segment, a contiguous segment of length $P$ in the first row is left empty as a sample collection area—this area is not counted as part of the experimental base. As a result, the base forms a “concave” shape. For example, the figure below shows a selection scheme. The region within the bold border is the experimental base. It covers a $2 \times 5$ area, and in the first row, a sample collection area of length $2$ is selected; its suitability values are $-4$ and $-5$ respectively.  Note: $Q$ and $P$ can be chosen arbitrarily within the range of $N$, but a sample collection area must be set, and there must be base cells on both the left and right sides of the sample collection area within the first row. 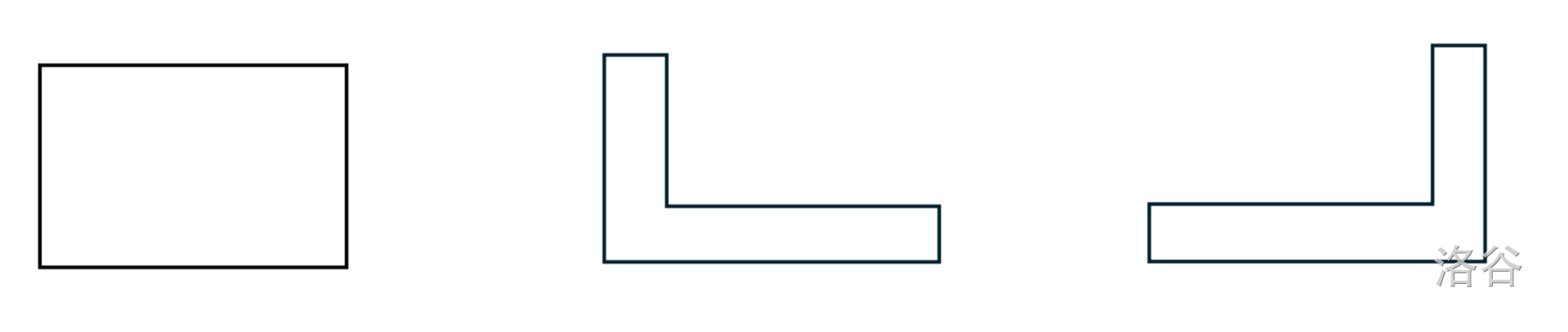Therefore, the following base shapes are not allowed:  The sum of the suitability values of all rectangular plots occupied by the experimental base is called the suitability of the base. Scientists hope to maximize this suitability and have assigned the site selection task to Xiao Keke. Please write a program to determine the optimal base location.

The first line contains an integer $N$ ($3 < N < 2000$), indicating the size of the landing zone is $2 \times N$. The next two lines each contain $N$ integers (each with absolute value at most $10^6$), representing the suitability values of the corresponding rectangular plots, separated by single spaces.

Output a single line with an integer $M$, the suitability of the determined experimental base.

Constraints are given in the input format. Translated by ChatGPT 5