P2551 [AHOI2001] Huaxia 60 Fighter Jet

The Huaxia 60 supersonic fighter jet is one of the most maneuverable fighters in the world today. A key issue in combat is how to climb/dive from the current flight altitude and speed to a designated altitude and achieve a designated speed in the shortest time to gain a superior combat position. Assume that the Huaxia 60 is allowed to perform only the following three basic maneuvers, and a new basic maneuver can only start after the previous one is completed. Thus, a flight can be represented as a sequence composed of these three basic maneuvers. (1) Maintain the current speed and perform a constant-speed climb until the flight altitude increases by $\Delta h$ feet. (2) Perform horizontal acceleration until the speed increases by 1 Mach (1 Mach $\approx 1200$ km/h). (3) Perform a vertical dive by $\Delta h$ feet, during which the flight speed increases by 1 Mach. Also assume that the initial flight speed and the speed at the beginning of each basic maneuver are integer multiples of 1 Mach and do not exceed 6 Mach; the initial flight altitude and the altitude at the beginning of each basic maneuver are integer multiples of $\Delta h$ feet (where $\Delta h$ is an integer). Experimental studies show that the time required to complete the above three basic maneuvers varies with different altitudes $H$ and initial speeds $V$. Tables 1–3 give the required times when $\Delta h = 15000$ feet and the maximum flight altitude is $75000$ feet. 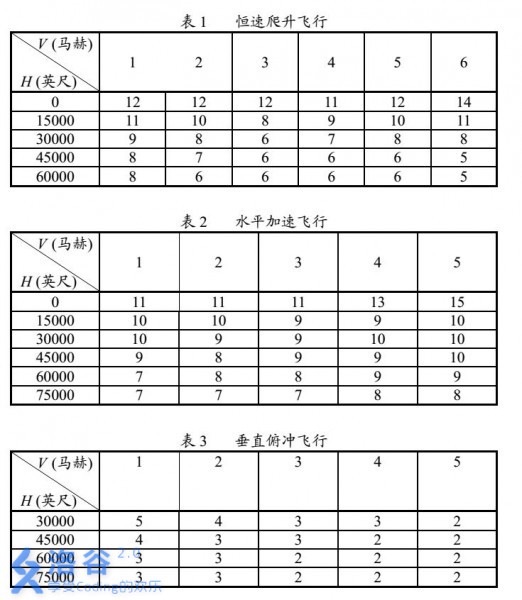Based on the data in Tables 1–3, the shortest time for the Huaxia 60 to reach the flight state $H=75000$ feet, $V=6$ Mach starting from $H=0$ feet, $V=1$ Mach is 79 seconds, and the corresponding sequence of maneuvers is:  (1) Constant-speed climb to $H=15000$ feet, $V=1$ Mach. (2) Perform two consecutive horizontal accelerations to $H=15000$ feet, $V=3$ Mach. (3) Perform four consecutive constant-speed climbs to $H=75000$ feet, $V=3$ Mach. (4) Horizontal acceleration to $H=75000$ feet, $V=4$ Mach. (5) Perform two consecutive vertical dives to $H=45000$ feet, $V=6$ Mach. (6) Perform two consecutive constant-speed climbs to $H=75000$ feet, $V=6$ Mach. Now Xiao Ming is flying the Huaxia 60 at $V_1$ Mach at altitude $H_1$ feet. The squadron commander orders him to fly at $V_2$ Mach at altitude $H_2$ feet. Please write a program to decide how to fly so that the order is completed in the least time.


The output contains two lines. - The first line contains the time required by your optimal plan. - The second line contains the action sequence of the optimal plan (use R for constant-speed climb, A for horizontal acceleration, and D for vertical dive). No extra characters (including whitespace) are allowed on the second line.

Translated by ChatGPT 5