P2585 [ZJOI2006] Three-Color Binary Tree

A binary tree can be represented as a character sequence consisting of $0$, $1$, and $2$ according to the following rules, which we call the "binary tree sequence $S$": $$ S= \begin{cases} 0 & \text{indicates that this node has no child} \\ 1S_1 & \text{indicates that this node has one child, and } S_1 \text{ is the binary tree sequence of its subtree} \\ 2S_1S_2 & \text{indicates that this node has two children, where } S_1 \text{ and } S_2 \text{ are the binary tree sequences of its two subtrees} \end{cases} $$ 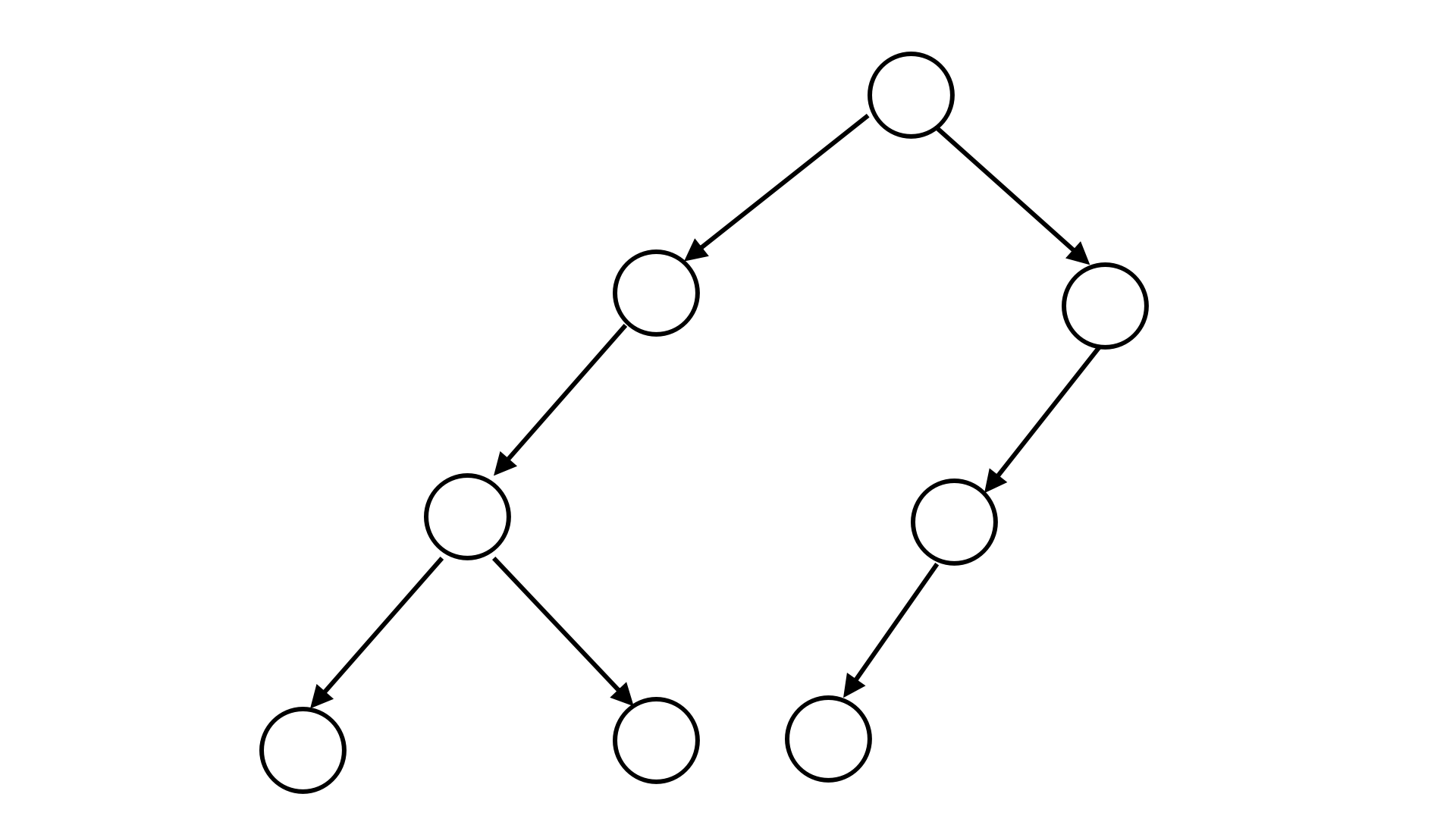For example, the binary tree shown in the figure below can be represented by the binary tree sequence $S=\texttt{21200110}$.  Your task is to color the nodes of a binary tree. Each node can be colored red, green, or blue. A node must have a different color from each of its children, and if it has two children, then the two children must also have different colors. Given the binary tree sequence of a tree, determine the maximum and minimum number of nodes that can be colored green.

The input contains a single line with a string $s$, which represents the binary tree sequence.

Output a single line with two numbers, indicating the maximum and then the minimum number of nodes that can be colored green.

Constraints For all test points, it is guaranteed that $1 \le |s| \le 5 \times 10^5$, and $s$ contains only the characters `0` `1` `2`. Translated by ChatGPT 5