P2591 [ZJOI2009] Functions

There are $N$ continuous functions $f_i(x)$, where $1 \le i \le N$. If for any unequal $i, j$ with $1 \le i, j \le N$, there exists exactly one $x$ such that $f_i(x) = f_j(x)$, and there exist infinitely many $x$ such that $f_i(x) < f_j(x)$, and for any $i, j, k$ with $1 \le i < j < k \le N$, there does not exist $x$ such that $f_i(x) = f_j(x) = f_k(x)$, then these $N$ continuous functions are said to satisfy the condition.  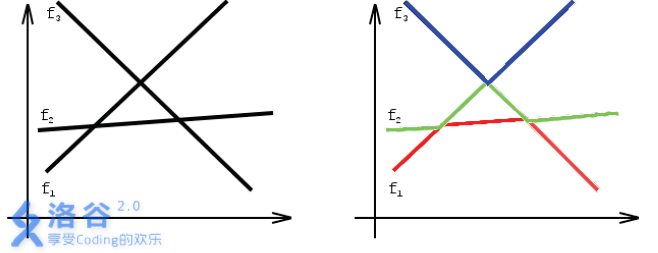As shown in the left figure, there are $3$ functions that satisfy the condition; on the far left, from bottom to top, they are $f_1, f_2, f_3$. In the right figure, the red part is the lowest layer of the entire graph, which we call the first layer. Similarly, the green part is the second layer, and the blue part is the third layer. Note that, in the right figure, the left segment of the first layer belongs to $f_1$, the middle segment belongs to $f_2$, and the last segment belongs to $f_3$. For the second layer, the left segment belongs to $f_2$, the next segment belongs to $f_1$, the next segment belongs to $f_3$, and the last segment belongs to $f_2$. Therefore, we say the first layer is divided into three segments, and the second layer is divided into four segments. Similarly, the third layer is divided into only two segments. Given $N$ functions that satisfy the conditions above, find the minimum possible number of segments that the $K$-th layer can consist of.

One line containing two integers $N$, $K$.

One line containing a single integer: the minimum number of segments of the $K$-th layer among the $N$ functions.

For $100\%$ of the testdata, $1 \le K \le N \le 100$. Translated by ChatGPT 5