P2597 [ZJOI2012] Disaster

Amiba is Xiaoqiang’s good friend. Amiba and Xiaoqiang are catching grasshoppers on the prairie. Xiaoqiang suddenly thinks that if grasshoppers were caught to extinction, then the birds that eat grasshoppers would starve, and the raptors that prey on those birds would also go extinct, triggering a chain of ecological disasters. Amiba, who has studied biology, tells Xiaoqiang that the prairie is an extremely stable ecosystem. If grasshoppers go extinct, birds can still eat other insects, so the extinction of one species does not necessarily cause a major disaster.

Let’s look at this problem from a more professional perspective. We use a directed graph called a food web to describe the relationships between species: - A food web has $n$ vertices, representing $n$ species, numbered from $1$ to $n$. - If species $x$ can eat species $y$, then draw a directed edge from $y$ to $x$. - The graph has no cycles. - Some vertices have no outgoing edges; these are producers that can survive via photosynthesis. - Vertices with outgoing edges are consumers; they must survive by eating other species. - If all the foods of a consumer go extinct, it will go extinct as well. We define the “disaster value” of a species in the food web as the number of species that would go extinct along with it if it suddenly went extinct. 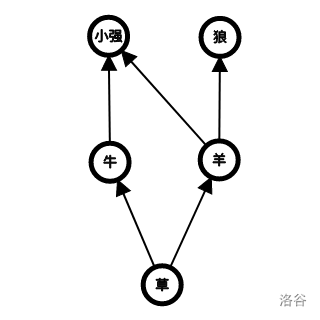For example: on a grassland, the relationships between species are as follows  If Xiaoqiang and Amiba scare all the sheep to death, then the wolves will go extinct due to lack of food, while Xiaoqiang and Amiba can survive by eating cows, and cows can survive by eating grass. Thus, the disaster value of sheep is $1$. However, if the grass suddenly went extinct, then all $5$ species on the grassland would be affected, so the disaster value of grass is $4$. Given a food web, you are required to compute the disaster value for each species.

The first line contains an integer representing the number of vertices $n$ in the food web. From the $2$-nd to the $(n + 1)$-st line, each line contains several distinct integers. The $(i + 1)$-st line lists integers $a_{i, j}$ indicating that species $i$ can eat species $a_{i, j}$. Each line ends with an integer $0$ marking the end of that line.

Output $n$ lines, one integer per line. On the $i$-th line, output the disaster value of species $i$.

### Sample 1 Explanation The sample input describes the example in the problem statement. ### Constraints - For $50\%$ of the testdata, it is guaranteed that $n \leq 10^4$. - For $100\%$ of the testdata, it is guaranteed that $1 \leq n \leq 65534$, $1 \leq a_{i, j} \leq n$, the input file size does not exceed $1$ MB, and the graph has no cycles. Translated by ChatGPT 5