P2674 Qupa's Number Game T2 - Polygonal Numbers

In the Kingdom of Numbers, there is a special class of numbers called polygonal numbers. King $1$ also decreed that marriages between numbers can only happen within the same type of polygonal numbers. (Please don't complain about this rule...) Qupa became very curious about this phenomenon. Seeing the couple $36$ and $10$ taking a walk, Qupa asked $36$ which kind of polygonal number it was. But $36$ patted its head and said, "I don't know either. Go ask the king." It seems the citizens do not know which polygonal numbers they are, and King $1$ is worried. King $1$ only knows how to compute polygonal numbers, but how should he explain this to the citizens? He decides to explain it this way: any integer that can be arranged into a regular polygon is a polygonal number. Polygonal numbers include triangular numbers, square numbers, pentagonal numbers, hexagonal numbers, and so on.

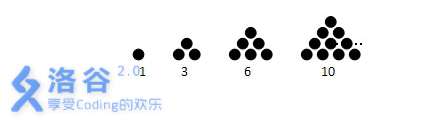
This is a pattern-finding problem. Please discover the pattern yourself to practice mathematical induction!! Let’s take triangular numbers as an example: the numbers $1$, $3$, $6$, $10$ in the figure are triangular numbers.  Task: determine which kinds of polygonal numbers $N$ belongs to (assume $N$ is a $K$-gonal number). For example, we can find that $36$ is both a triangular number and a square number. If it is not a polygonal number, output Poor + that number. If it is multiple types of polygonal numbers at the same time, output the smallest $K$ and the second smallest $K$. Each input file contains $ng$ test cases.

First a number $ng$, then $ng$ lines, each containing one integer.

Output $ng$ lines. For each $N$, output the corresponding $K_1$ and $K_2$. If $N$ is not a polygonal number, output Poor + that number (no spaces in between).

### Constraints and Notes For $20\%$ of the testdata, $1 \le K_1, K_2 \le 6$. For $100\%$ of the testdata, $1 \le N \le 10^6$, $1 \le ng \le 10^2$. If $N$ is multiple types of polygonal numbers at the same time, let $K_1$ be the smallest $K$, and $K_2$ be the second smallest $K$. King $1$: "Can you discover the pattern that square numbers are just perfect squares? To make it easier to understand, I’ll provide a table of the first few polygonal numbers." (From the table you can see that a regular hexagon does not include the very center point, and similarly for others.) | Natural numbers | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | | :-: | :-: | :-: | :-: | :-: | :-: | :-: | :-: | :-: | | Triangular numbers | $1$ | $3$ | $6$ | $10$ | $15$ | $21$ | $28$ | $36$ | | Square numbers | $1$ | $4$ | $9$ | $16$ | $25$ | $36$ | $49$ | $64$ | | Pentagonal numbers | $1$ | $5$ | $12$ | $22$ | $35$ | $51$ | $70$ | $92$ | | Hexagonal numbers | $1$ | $6$ | $15$ | $28$ | $45$ | $66$ | $91$ | $120$ | Translated by ChatGPT 5