P2691 Escape

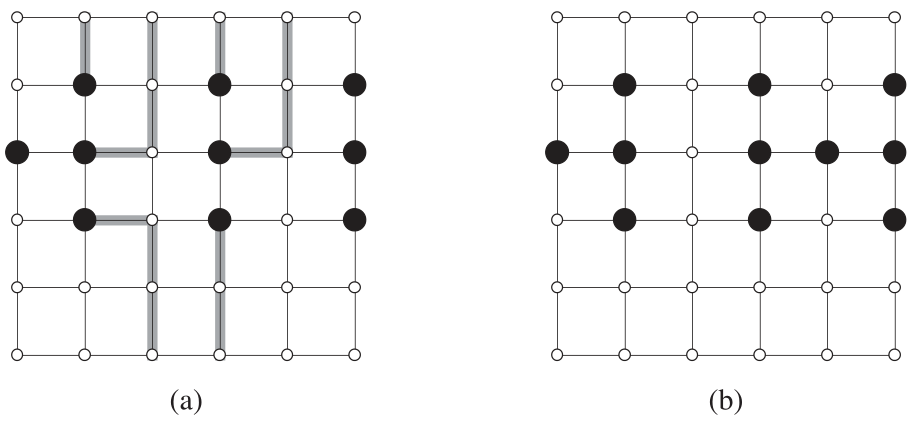
Translated from CLRS Problem 26-1: Escape problem. In an $n \times n$ grid, there are $m$ starting points $(x_1, y_1)$, $(x_2, y_2)$, $\dots$, $(x_m, y_m)$. Determine whether it is possible to find a path for each starting point to the boundary such that these $m$ paths are pairwise disjoint (that is, no two paths share any point).  Black dots indicate starting points, and other points are white. The found paths are shown with bold lines. In figure (a), there exist $m$ valid paths; in figure (b), there do not.

The first line contains an integer $n$ ($1 \le n \le 35$). The second line contains an integer $m$ ($1 \le m \le n^2$). Each of the following $m$ lines, the $(i + 2)$-th line, contains two integers $x_i$ and $y_i$, meaning that the point at row $x_i$, column $y_i$ is a starting point. The starting points are guaranteed to be distinct.

Output a single line. If an escape exists, output `YES`; otherwise, output `NO`.

Translated by ChatGPT 5