P2751 [IOI 1996 / USACO4.2] Job Processing

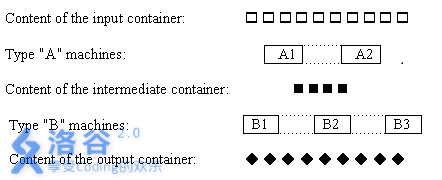
A factory production line is producing a product that requires two types of operations: operation $A$ and operation $B$. Only some machines can perform each operation.  The figure above shows the organization of a production line operating as described below. $A$-type machines take workpieces from the input buffer, apply operation $A$, and store the resulting intermediate products in the buffer. $B$-type machines take intermediate products from the buffer, apply operation $B$, and store the final products in the output buffer. All machines work in parallel and independently, and each buffer has unlimited capacity. Each machine may have a different efficiency; a machine requires a fixed amount of time to complete one operation. Given the processing time of each machine for one operation, compute the minimal total time to finish all $A$ operations, and the minimal total time to finish all $B$ operations. Note: 1. In one operation, a machine processes exactly one workpiece. 2. “Total time” means the latest finishing time (makespan).

The first line contains three space-separated integers: $N$, the number of workpieces ($1 \leq N \leq 1000$); $M_1$, the number of $A$-type machines ($1 \leq M_1 \leq 30$); $M_2$, the number of $B$-type machines ($1 \leq M_2 \leq 30$). The second line contains $M_1$ integers, the time each $A$-type machine takes to complete one operation; followed by $M_2$ integers, the time each $B$-type machine takes to complete one operation. All operation times for $A$-type and $B$-type machines are integers in $[1, 20]$.

Output a single line with two integers: the minimal total time to complete all $A$ operations, and the minimal total time to complete all $B$ operations ($A$ operations must be completed before $B$ operations).

Problem translation from NOCOW. USACO Training Section 4.2. Translated by ChatGPT 5