P2752 [USACO4.3] Street Race

Figure 1 shows a course for a street race. There are several intersections (labeled by the integers from $0$ to $N$) and arrows that connect these intersections. Intersection $0$ is the start, and intersection $N$ is the finish. The arrows indicate one-way streets. Runners can move from one intersection to another along the streets (only in the direction of the arrows). When a runner is at an intersection, they may choose any outgoing street from that intersection.  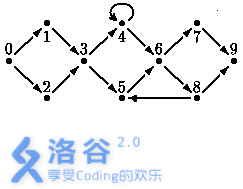Figure 1: A street with $10$ intersections. A valid course has the following properties: 1. Every intersection is reachable from the start. 2. The finish is reachable from any intersection. 3. The finish has no outgoing streets. Runners do not have to pass through all intersections to complete the race. However, some intersections must be passed on every possible route (called "unavoidable"). In the example above, these intersections are $0$, $3$, $6$, $9$. For a given valid course, your program must determine the set of unavoidable intersections, excluding the start and the finish. Assume the race is to be held over two days. To achieve this, the original course must be split into two courses, one for each day. On day 1, the start is intersection $0$ and the finish is an "intermediate intersection"; on day 2, the start is that intermediate intersection and the finish is intersection $N$. For a given valid course, your program must determine the set of "splitting points". If a valid course $C$ can be divided by an intersection $S$ into two parts that are both valid, $S$ is different from both the start and the finish, and the two parts satisfy the following conditions: (1) they share no streets; (2) their only common point is $S$, with $S$ serving as the finish of one and the start of the other; then $S$ is called a "splitting point". In the example, only intersection $3$ is a splitting point.

The input describes a valid course with at most $50$ intersections and $100$ one-way streets. There are $N+2$ lines. In the first $N+1$ lines, line $i$ lists the streets that start from the intersection numbered $i-1$, and each number denotes a destination. Each line ends with `-2`. The last line contains a single number `-1`.

The first line: the number of unavoidable intersections, followed by their indices in increasing order. The second line: the number of splitting points, followed by their indices in increasing order.

Problem translation from NOCOW. USACO Training Section 4.3. Translated by ChatGPT 5