P2783 The God of Organic Chemistry Occasionally Cheats

The coach of the XS Middle School chemistry contest team is a big fan of Hearthstone. One day, he was invigilating while playing Hearthstone, and you, being a programming contest pro, also came to watch. However, your chemistry-contest buddy turned to you for help. "How do I solve Problem 1354?" — he asked in sign language.

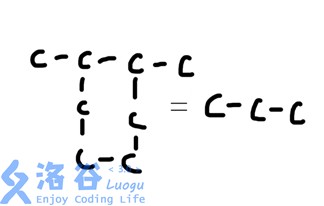
You flip to that problem: given a hydrocarbon that contains only single bonds (an intuitive explanation for middle schoolers: a bunch of carbons connected by single lines, and every line is a single bond). Then Ragnaros the Firelord purified all cycles with his flames (???). Every cyclic carbon structure is contracted into a single carbon, as shown in the figure.  Next, for multiple specified pairs of carbons, compute how many carbons are between them in total, as illustrated (this illustration is unrelated to the one above).  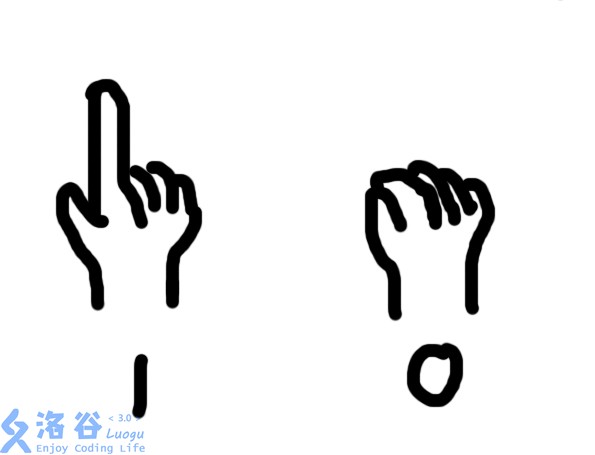But since this is during an exam, you can only tell your buddy the answer using sign language. You decide to represent the final answer in binary, as shown (don’t mind it; it’s not really related to the problem).  In short: you are given an undirected graph with $n$ vertices and $m$ edges. Contract every cycle in the graph into a single vertex. After this transformation, for each query asking about two vertices, find how many vertices lie between them.

- The first line contains two integers $n$, $m$, meaning there are $n$ vertices and $m$ bonds. - The next $m$ lines each contain two integers $u$, $v$, indicating there is a bond between carbon $u$ and carbon $v$. - The next line contains an integer $tot$, the number of queries. - The next $tot$ lines each contain two integers $a$, $b$, denoting the indices of the two queried carbons.

Output $tot$ lines, each containing a binary number representing the answer.

The two queried carbons do not lie on a cycle. # Constraints For $100\%$ of the testdata, $1 < n \le 10^4$, $1 < m \le 5 \times 10^4$. Translated by ChatGPT 5