P2808 [JOI2014 Preliminary Round] Xiaolongbao

JOI’s lunch is xiaolongbao bought at a Chinese restaurant. This dish has a wrapper made from wheat flour enclosing filling and hot soup; when eating, the hot soup may splash.

The xiaolongbao set that JOI ordered consists of $N$ xiaolongbao with different fillings. The $N$ xiaolongbao are arranged in a row at equal intervals, numbered $1$ to $N$. The distance between the $i$-th and $j$-th xiaolongbao is the absolute value $\vert i-j\vert$. JOI eats the xiaolongbao in some order. Initially, the deliciousness of every xiaolongbao is $0$. When eating the $i$-th xiaolongbao, soup splashes outward; all xiaolongbao whose distance from the $i$-th xiaolongbao is at most $D_i$ are splashed, and each splashed xiaolongbao has its deliciousness increased by $A_i$. That is, when eating the $i$-th xiaolongbao, if the $j\ (1\le j\le N$ and $i-D_i\le j\le i+D_i)$-th xiaolongbao has not yet been eaten, then the deliciousness of the $j$-th xiaolongbao increases by $A_i$.  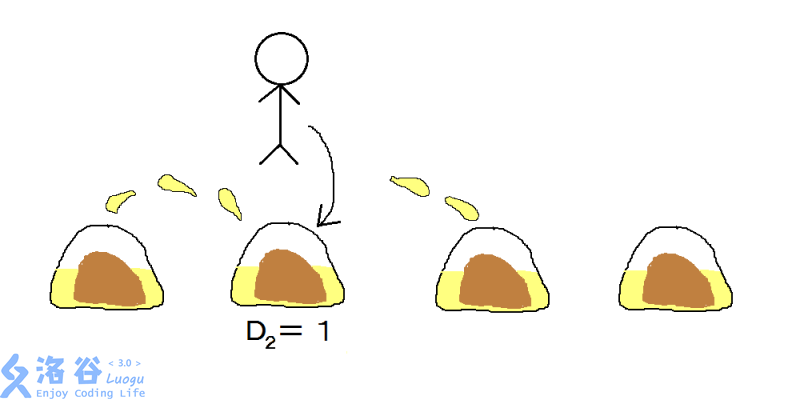JOI will choose the eating order to maximize the total deliciousness of the xiaolongbao eaten.

The input consists of three lines. The first line contains an integer $N\ (1\le N\le 100)$. The second line contains $N$ integers $D_1,D_2,\dots,D_N\ (0\le D_i\le 7)$, separated by spaces. The third line contains $N$ integers $A_1,A_2,\dots,A_N\ (0\le A_i\le 1000)$, separated by spaces.

Output one line: the maximum possible total deliciousness of the xiaolongbao eaten by JOI.

Explanation for Sample $1$: If JOI eats in the order $5\rightarrow 3\rightarrow 1\rightarrow 2\rightarrow 4$, the total deliciousness is $20$. It can be proven that no eating order yields a total exceeding $20$. This problem is Problem $6$ of the 2014 Japanese Olympiad in Informatics (JOI) Preliminary Round. Translated by ChatGPT 5