P2809 hzwer Loves Origami
Description
hzwer bought a magical little paper strip. Initially, it consists of $N$ cells, and each cell has an integer $N_i$ on it. Obviously, there is a dividing line between every two adjacent cells. hzwer can choose any dividing line and fold the entire strip to the left. If two cells overlap after folding, the number on the resulting cell equals the sum of the two original cells; otherwise, the numbers remain unchanged. hzwer can also reverse the entire strip; after reversing, the number of the $i$-th cell becomes the number of the $(N - i + 1)$-th cell.
hzwer wants to obtain an ideal strip with $M$ cells and values $m_i$. Determine whether it is possible to transform the initial strip into the ideal strip by performing the above operations any number of times.
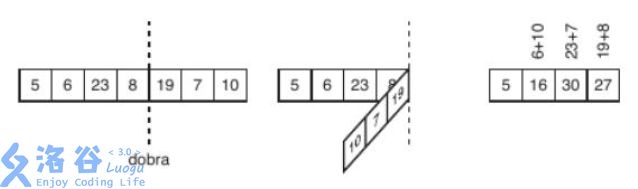
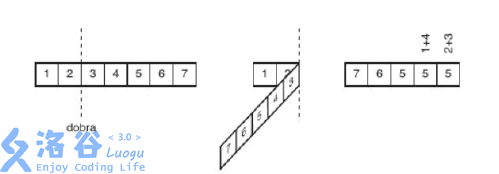
Input Format
Multiple test cases, at most $5$ groups. Each test case consists of four lines:
- The first line contains an integer $N$, the number of cells in the initial strip.
- The second line contains $N$ integers, the initial values $N_i$ of each cell.
- The third line contains an integer $M$ ($M \le N$), the number of cells in the ideal strip.
- The fourth line contains $M$ integers, the values $m_i$ on the ideal strip.
Output Format
For each test case, output one letter: `S` means feasible, and `N` means infeasible.
Explanation/Hint
For $70\%$ of the testdata, $N \le 10$.
For $100\%$ of the testdata, $1 \le N \le 15$.
Translated by ChatGPT 5