P2827 [NOIP 2016 Senior] Earthworms

NOIP 2016 Senior D2T2.

In this problem, we use the symbol $\lfloor c \rfloor$ to denote the floor of $c$. For example, $\lfloor 3.0 \rfloor = \lfloor 3.1 \rfloor = \lfloor 3.9 \rfloor = 3$. The Cricket Kingdom is suffering from an earthworm outbreak! Even the fleas from the neighboring Flea Kingdom can’t handle the earthworms. The Cricket King has no choice but to invite the Divine Blade Master to help eliminate them. There are currently $n$ earthworms in the Cricket Kingdom (where $n$ is a positive integer). Each earthworm has a length. Let the length of the $i$-th earthworm be $a_i \,(i=1,2,\dots,n)$, and all lengths are guaranteed to be non-negative integers (i.e., earthworms with length $0$ may exist). Every second, the Divine Blade Master will accurately find the longest earthworm among all earthworms (if there are multiple, choose any one) and cut it in half. The cutting position is determined by a constant $p$ (a rational number satisfying $0 < p < 1$). Suppose the length of this earthworm is $x$. The master will cut it into two earthworms with lengths $\lfloor p x \rfloor$ and $x - \lfloor p x \rfloor$. In particular, if either of these numbers equals $0$, that earthworm of length $0$ is also kept. In addition, except for the two newly created earthworms, the lengths of all other earthworms will increase by $q$ (a non-negative integer constant). The Cricket King knows this is not a long-term solution, because not only will the number of earthworms increase, but they will also become longer. The king decides to seek help from a mysterious figure with great power, but the reinforcements will take $m$ seconds to arrive... (where $m$ is a non-negative integer). The king wants to know the situation within these $m$ seconds. Specifically, he wants to know: - Within $m$ seconds, for each second, the length of the earthworm that is cut, measured just before it is cut (there are $m$ numbers). - After $m$ seconds, the lengths of all earthworms (there are $n + m$ numbers). Of course, the Cricket King knows how to do this! But he wants to test you.

The first line contains six integers $n,m,q,u,v,t$, where: the meanings of $n,m,q$ are as in [Description]; $u,v,t$ are positive integers; you need to compute $p = u / v$ yourself (guaranteed $0 < u < v$); $t$ is an output parameter, whose meaning will be explained in [Output Format]. The second line contains $n$ non-negative integers, namely $a_1, a_2, \dots, a_n$, the initial lengths of the $n$ earthworms. Between any two adjacent numbers on the same line, there is exactly one space. 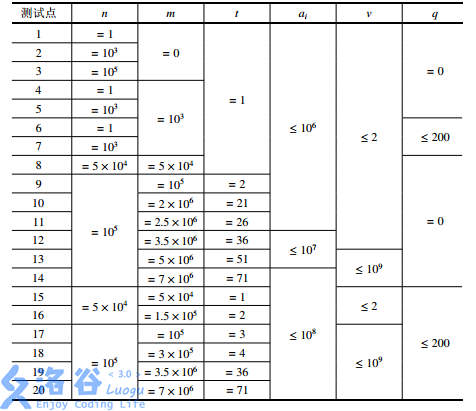It is guaranteed that $1 \leq n \leq 10^5$, $0 \leq m \leq 7 \times 10^6$, $0 < u < v \leq 10^9$, $0 \leq q \leq 200$, $1 \leq t \leq 71$, $0 \leq a_i \leq 10^8$.

On the first line, output $\left\lfloor \frac{m}{t} \right\rfloor$ integers. In chronological order, output the length (just before being cut) of the earthworm cut at time $t$, $2t$, $3t$, … . On the second line, output $\left\lfloor \frac{n+m}{t} \right\rfloor$ integers: after $m$ seconds, output the earthworm lengths in non-increasing order, specifically the $t$-th, $2t$-th, $3t$-th, … largest lengths. Between any two adjacent numbers on the same line, there is exactly one space. Even if a line has no numbers to output, you must still output a blank line. Please read the samples to better understand this format.

Sample Explanation 1 Before the Divine Blade Master arrives: the lengths of $3$ earthworms are $3, 3, 2$. After $1$ second: one earthworm of length $3$ is cut into two earthworms of lengths $1$ and $2$; the other earthworms increase by $1$. In the end, the $4$ earthworms have lengths $(1,2), 4, 3$. Parentheses mean an earthworm at that position has just been cut. After $2$ seconds: one earthworm of length $4$ is cut into $1$ and $3$. The $5$ earthworms’ lengths are: $2, 3, (1,3), 4$. After $3$ seconds: one earthworm of length $4$ is cut. The $6$ earthworms’ lengths are: $3, 4, 2, 4, (1,3)$. After $4$ seconds: one earthworm of length $4$ is cut. The $7$ earthworms’ lengths are: $4, (1,3), 3, 5, 2, 4$. After $5$ seconds: one earthworm of length $5$ is cut. The $8$ earthworms’ lengths are: $5, 2, 4, 4, (1,4), 3, 5$. After $6$ seconds: one earthworm of length $5$ is cut. The $9$ earthworms’ lengths are: $(1,4), 3, 5, 5, 2, 5, 4, 6$. After $7$ seconds: one earthworm of length $6$ is cut. The $10$ earthworms’ lengths are: $2, 5, 4, 6, 6, 3, 6, 5, (2,4)$. Therefore, within $7$ seconds, the lengths of the cut earthworms are $3, 4, 4, 4, 5, 5, 6$ in order. After $7$ seconds, all earthworm lengths in non-increasing order are $6, 6, 6, 5, 5, 4, 4, 3, 2, 2$. Sample Explanation 2 In this testdata, only $t = 2$ differs from the previous one. You only need to output one number every two numbers on each line. Although the last $6$ on the first line is not output, the second line must restart counting from the second number. Sample Explanation 3 In this testdata, only $t = 9$ differs from the previous one. Note that there are no numbers to output on the first line, but you must still print a blank line. Constraints  Translated by ChatGPT 5