P2860 [USACO06JAN] Redundant Paths G

为了从 $F(1\le F\le 5,000)$ 个牧场（编号为 $1$ 到 $F$）中的一个到达另一个牧场，贝西和其他牛群被迫经过腐烂苹果树附近。奶牛们厌倦了经常被迫走特定的路径，想要修建一些新路径，以便在任意一对牧场之间总是有至少两条独立的路线可供选择。目前在每对牧场之间至少有一条路径，他们希望至少有两条。当然，他们只能在官方路径上从一个牧场移动到另一个牧场。 给定当前 $R(F-1\le R\le 10,000)$ 条路径的描述，每条路径恰好连接两个不同的牧场，确定必须修建的最少新路径数量（每条新路径也恰好连接两个牧场），以便在任意一对牧场之间至少有两条独立的路线。若两条路线不使用相同的路径，即使它们沿途访问相同的中间牧场，也被视为独立的。 在同一对牧场之间可能已经有多条路径，你也可以修建一条新路径连接与某条现有路径相同的牧场。

第 $1$ 行：两个用空格分隔的整数：$F$ 和 $R$。 第 $2$ 行到第 $R+1$ 行：每行包含两个用空格分隔的整数，表示某条路径的两个端点牧场。

第 $1$ 行：一个整数，表示必须修建的新路径数量。

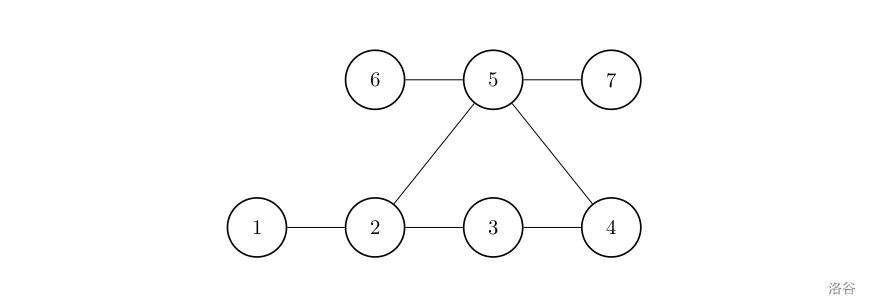
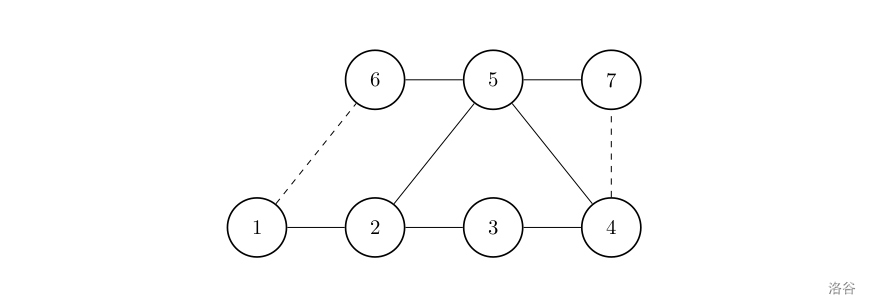
样例解释： 路径的一个可视化图如下：  从 $1$ 到 $6$ 和从 $4$ 到 $7$ 修建新路径满足条件。  检查一些路线： - $1 \to 2$：$1 \to2$ 和 $1 \to6 \to5 \to2$ - $1 \to 4$：$1 \to2 \to3 \to4$ 和 $1 \to6 \to5 \to4$ - $3 \to 7$：$3 \to4 \to7$ 和 $3 \to2 \to5 \to7$ 事实上，每对牧场之间都由两条路线连接。 添加其他路径也可能解决问题（例如从 $6$ 到 $7$ 的路径）。然而，添加两条路径是最少的。 （由 ChatGPT 4o 翻译）