P3219 [HNOI2012] 三角形覆盖问题

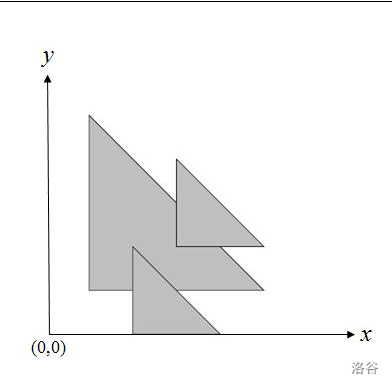
二维平面中，给定 $N$ 个等腰直角三角形（每个三角形的两条直角边分别平行于坐标轴，斜边从左上到右下）。我们用三个非负整数 $(x,y,d)$ 来描述这样一个三角形，三角形三个顶点的坐标分别为 $(x,y)$，$(x+d,y)$ 和 $(x,y+d)$。要求计算这 $N$ 个三角形所覆盖的总面积。例如，下图有 $3$ 个三角形，覆盖的总面积为 $11.0$。 

输入文件第一行为一个正整数 $N$，表示三角形的个数。 接下来的 $N$ 行每行有用空格隔开的三个非负整数 $x,y,d$，描述一个三角形的顶点坐标，分别为 $(x,y)$，$(x+d,y)$，$(x,y+d)$，其中 $x,y,d$ 满足 $0 \le x,y,d \le 10^6$。

仅包含一行，为一个实数 $S$，表示所有三角形所覆盖的总面积，输出恰好保留一位小数。输入数据保证 $S \le 2^{31}$。

对于 $50\%$ 的数据，$1 \le N \le 500$；\ 对于 $100\%$ 的数据，$1 \le N \le 10^4$。