P3219 [HNOI2012] Triangle Coverage Problem

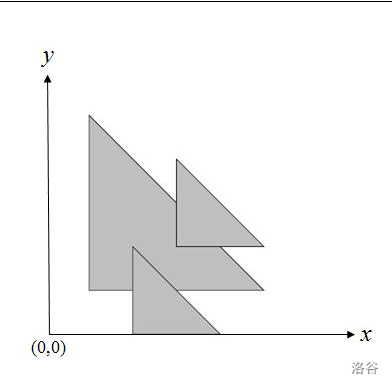
In the two-dimensional plane, you are given $N$ isosceles right triangles (each triangle’s two legs are parallel to the coordinate axes, and the hypotenuse goes from top-left to bottom-right). We use three non-negative integers $(x, y, d)$ to describe such a triangle. The coordinates of its three vertices are $(x, y)$, $(x+d, y)$, and $(x, y+d)$. Compute the total area covered by these $N$ triangles. For example, in the figure below, there are $3$ triangles, and the total covered area is $11.0$. 

The first line contains a positive integer $N$, indicating the number of triangles. Each of the next $N$ lines contains three space-separated non-negative integers $x, y, d$, describing a triangle whose vertices are $(x, y)$, $(x+d, y)$, and $(x, y+d)$, where $x, y, d$ satisfy $0 \le x, y, d \le 10^6$.

Output a single line containing a real number $S$, the total area covered by all triangles, with exactly one decimal place. It is guaranteed that $S \le 2^{31}$.

For $50\%$ of the testdata, $1 \le N \le 500$. For $100\%$ of the testdata, $1 \le N \le 10^4$. Translated by ChatGPT 5