P3244 [HNOI2015] Fallen Memories of Maple Echo

“Hengyi, do you believe that souls exist?” Guo Hengyi and Yao Fengqian were strolling along the street in Maple Echo Village. Watching the fluttering red maple leaves, Fengqian suddenly asked this question. “I guess I do. Otherwise, what are we—just a lump of flesh? Without souls... we couldn’t have seen your sister again, right?” Hengyi gave a slightly offbeat answer. Fengqian smiled. “Then have you carefully observed maple leaves?” With that, Fengqian reached out and caught a falling maple leaf. “In fact, every maple leaf has a soul. Look, aren’t there many veins on a maple leaf? I’ve heard that there are some special points on a leaf, just like acupoints on a human body. The veins connect these acupoints. The maple tree’s soul flows through the root of each leaf, along these veins, slowly soaking into the acupoints and permeating the entire leaf. This is also why the veins are all one-way—souls can’t flow backward.” Hengyi nodded, half understanding. Fengqian continued. “Because of the soul, every maple leaf is unique. Also because of the soul, every leaf resembles its source—the maple tree itself. Even the vein pattern forms the shape of a tree. But if you look carefully, you’ll find that beyond the vein-tree there are other very fine veins. Although these veins are not on the tree, their directions still follow the direction of the soul’s flow, and there will never be a cycle that could cause reverse flow.” Hengyi suddenly thought of something. “So these veins could replace existing ones and appear on the vein-tree, right?” Fengqian closed her eyes. “Yes, exactly. The vein-tree is not unique. With slight deviations, the vein-tree might differ greatly, even on the very same leaf. Just like our story—the ending is not unique. Change a small choice, and the entire storyline may be completely altered.” “That’s so profound...” Hengyi stared at the red maple leaf, contemplating. Fengqian went on. “And that’s not all. No vein exists forever, nor disappears forever. This is true for both veins on the vein-tree and the fine veins outside it. Existing veins may break and vanish; vanished veins may reconnect. Everything is in eternal change, including the bonds between people. Perhaps one day, our bonds with everyone will be ruthlessly severed like veins. Perhaps we, too, will become ‘passersby in Maple Echo Village.’ Perhaps all this is inevitable—decided by the soul of the maple tree...” Tears shimmered in the corner of Fengqian’s eyes. Seeing this, Hengyi held her in his arms. “Don’t think like that, Fengqian. Even if some veins break, a new vein-tree may still form and still connect to the tree’s root. If so, our bond still exists—it only takes a slightly longer path. No matter what, I won’t leave you. Because you are the one I’ve sought my entire life—my true love!” Their eyes met. Fengqian smiled happily and buried her head in Hengyi’s embrace. From the maple forest on the distant mountain came the sound of the maples.

Assume there are $n$ acupoints on a maple leaf, numbered $1 \sim n$. Several directed veins connect these acupoints. The acupoints and veins form a directed acyclic graph—called the vein graph (for example, Figure $1$). The numbering of the acupoints ensures that acupoint $1$ has no incoming veins from other acupoints, that is, acupoint $1$ only has outgoing veins. As the story above suggests, this directed acyclic graph contains a tree-shaped subgraph: a tree rooted at acupoint $1$ that spans all $n$ acupoints—called a vein-tree (for example, the trees in Figure $2$ and Figure $3$ are both vein-trees of the vein graph given by Figure $1$). Note that there may be multiple vein-tree schemes in the vein graph. For example, Figure $2$ and Figure $3$ are two different vein-tree schemes for the vein graph in Figure $1$.  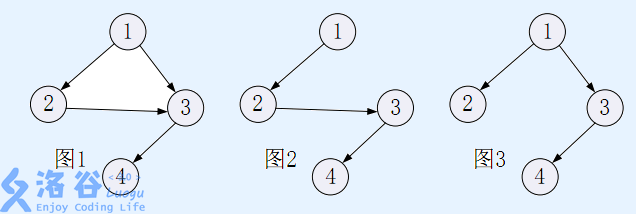A formal definition of a vein-tree is as follows: a vein-tree rooted at acupoint $r$ consists of all $n$ acupoints and $(n-1)$ veins. There are no cycles in the vein-tree, nor self-loops. Moreover, for every acupoint $s$ on the leaf, there exists a unique vein path contained in the vein-tree such that starting from acupoint $r$ and following this path you can reach acupoint $s$. Now we add one new vein, different from all existing veins, to the vein graph (note: veins connecting the same two acupoints but in opposite directions are considered different. For example, the vein from acupoint $3$ to $4$ is different from the vein from $4$ to $3$. Therefore, in Figure $1$, you cannot add a vein from $3$ to $4$, but you may add a vein from $4$ to $3$). This new vein may be a self-loop (for example, in Figure 1, a vein from $4$ to $4$ can be added). After adding this new vein, cycles formed by veins may appear in the new vein graph. Please compute the number of vein-tree schemes rooted at acupoint $1$ in the new vein graph after adding this vein. Since the number of schemes may be very large, output it modulo $(10^9+7)$.

The first line contains four integers $n, m, x, y$, representing the number of acupoints on the leaf, the number of veins, and that the vein to be added goes from acupoint $x$ to acupoint $y$. The next $m$ lines each contain two integers separated by a space, representing one existing vein. In line $i$, the two integers are $u_i$ and $v_i$, meaning the $i$-th vein goes from acupoint $u_i$ to acupoint $v_i$.

Output one line: the number of vein-tree schemes rooted at acupoint $1$ on the leaf after adding the vein from $x$ to $y$, modulo $(10^9+7)$.

For all testdata, it is guaranteed that: - $1 \leq n \leq 100000$. - $n - 1 \leq m \leq \min(200000, n(n - 1)/2)$. - $1 \leq x, y, u_i, v_i \leq n$. Fixed by Starrykiller. Translated by ChatGPT 5