P3257 [JLOI2014] Tiantian Cool Run

In the game Tiantian Cool Run, the most exciting part is probably the Super Bonus mode, where there are no obstacles and you can freely collect coins. Now you are to control the character to obtain as high a score as possible. The game interface is discretized into a grid with length from $1$ to $n$ and height from $1$ to $m$ (the starting point is $(0,1)$). Every cell has a gain in the range $(-1 \sim 1000)$, where $-1$ means the cell is impassable. The character runs from the start to the finish; along the way, they can jump to get a higher score, and can even perform consecutive jumps while in midair. Before the game starts, you may set the jump height and the number of consecutive jumps. The initial jump height is $1$, and the initial number of consecutive jumps is $1$ (up to a maximum of $5$). Upgrading jump height and the number of consecutive jumps both require a certain cost. Once the jump height is set, every jump will use this fixed height. A consecutive jump can only be used while descending. All actions happen at integer time steps. You must ensure that with the set jump height and number of consecutive jumps, the character cannot jump above the top boundary of the game.  From $(1,1)$, using one jump, the path passes through $(2,2),(3,3),(4,2),(5,1)$. 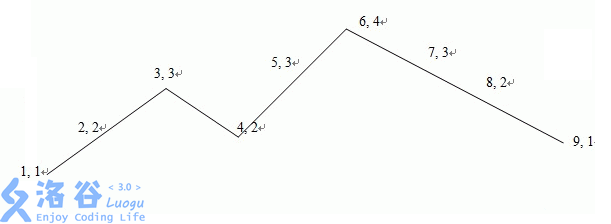Below is a jumping plan with the number of consecutive jumps equal to $2$ and jump height equal to $2$:  Starting to jump from $(1,1)$, the path goes through $(2,2),(3,3),(4,2)$, then uses a consecutive jump and passes through $(5,3),(6,4),(7,3),(8,2),(9,1)$. 

The first line contains four integers $n,m,cost_1,cost_2$. Here $n,m$ are as described above, and $cost_1,cost_2$ respectively denote the cost to increase the jump height by $1$ level and the cost to increase the number of consecutive jumps by $1$. Then follow $m$ lines, each containing $n$ integers. The integer in the $i$-th row and $j$-th column gives the gain at height $i$ and length $j$ in the map.

If it is impossible to reach the finish line, output `mission failed`. Otherwise, output one line with three integers: the maximum gain; among all settings achieving the maximum gain, the minimum number of consecutive jumps; and among those, the minimum jump height.

For $20\%$ of the testdata, $m=2$ and $1 \le n \le 10^5$. For the remaining $80\%$ of the testdata, $1 \le n \le 10000$, $2 < m \le 20$. Among them, for $20\%$ of the testdata it is guaranteed that $2 < n \le 10$, $1 \le m \le 10$. Translated by ChatGPT 5